Достаточно ли анализа гистограмм распределения и индексов воспроизводимости Cp, Cpk? Начинайте анализ с построения контрольных карт Шухарта!
Материал подготовил научный директор Центра AQT Григорьев С. П.
Бесплатный доступ к статьям нисколько не уменьшает ценности изложенных в них материалов.
В отделе обеспечения качества одной научно-производственной компании мне показали гистограмму распределения ключевого показателя качества, которую специалисты использовали при расследовании причин серьезной аварии, их доводы больше напоминали гадание на кофейной гуще. Никто понятия не имел о статистическом состоянии производственного процесса по этому показателю.
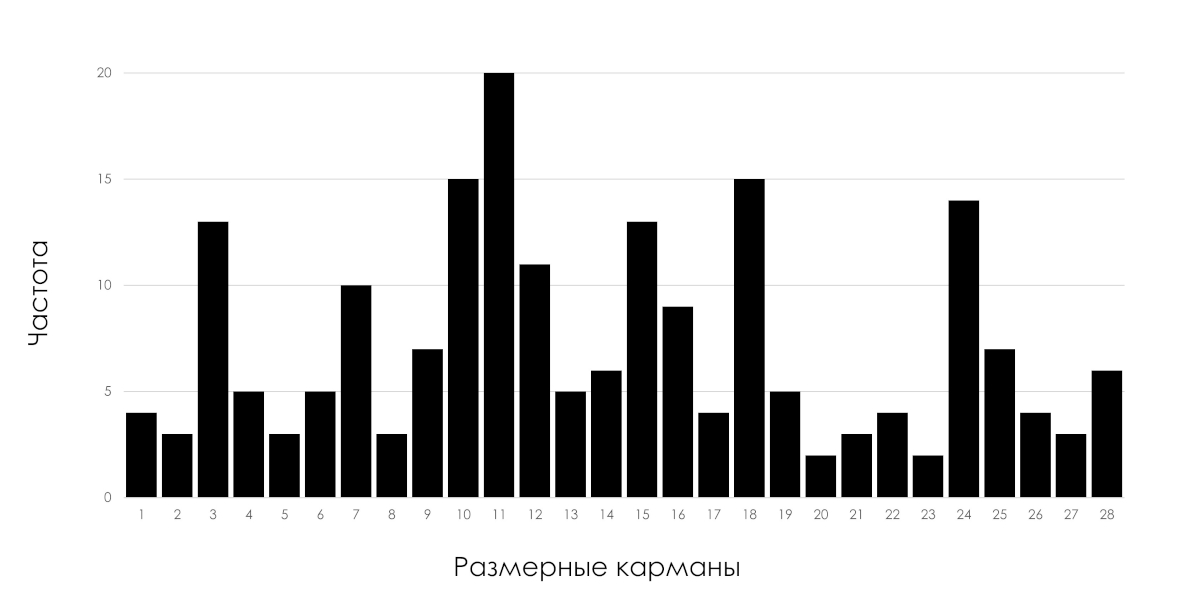
Рис. 1: Гистограмма распределениям ключевого показателя качества.
Почему это важно?! Авария - это следствие, а не причина.
Изображённая на рисунке выше гистограмма распределения показателя может быть результатом функционирования как статистически устойчивого (предсказуемого), так и статистически неустойчивого (непредсказуемого) процессов.
Если на производстве ведутся записи параметров деталей для этой гистограммы, почему не ведутся контрольные карты Шухарта для отслеживания статистического состояния хода процесса? Контрольные карты сообщили бы о разладке процесса производства, виновной в аварии детали, как только это стало возможным, даже если контрольный параметр детали всё ещё находился в границах поля допуска. У производственного персонала было бы основание остановить процесс производства до выяснения особой причины разладки и её устранения. По деталям, произведённым в период, захваченный разладкой процесса, нужно было принять решение пропускать их дальше или забраковать, подчёркиваю, даже при соответствии этих деталей полю допуска. Детали, произведённые процессом, находящимся в статистически неустойчивом (непредсказуемом) состоянии не являются однородными, они существенно различны. Границы допусков для определения однородности неприменимы. Важно понимать это для особо ответственных деталей.
От статистического состояния, в котором находится анализируемый процесс зависит выбор между двумя противоположными типами мероприятий по отношению к нему в целях его совершенствования. Смотрите подробное пояснении в статье " Природа вариабельности ".
Ниже представлено пояснение Эдвардса Деминга по проблеме интерпретации гистограмм плотностей распределения значений, ставшей поводом для этого кейса.
"Курсы по статистике часто начинаются с изучения распределений и их сравнения. Студентов ни на занятиях, ни в книгах не предупреждают о том, что для аналитических целей (таких как улучшение процесса) распределения и вычисление среднего, стандартного отклонения, значений хи-квадрат, t-статистики и т. д. бесполезны, если только данные не были получены для процесса в состоянии статистической управляемости
Соответственно, первый шаг при исследовании данных – понять, получены ли они в состоянии статистической управляемости. Самый легкий путь при анализе данных – это расположить точки в порядке их появления, чтобы понять, можно ли извлечь какую-либо пользу из распределения, образованного данными.
В качестве примера обратимся к распределению, которое, по-видимому, имеет наилучшие характеристики, но при этом не просто бесполезно, а вводит в заблуждение. На рис. 2 показано распределение результатов замеров 50 пружинок одного вида, используемых в фотоаппарате определенного типа. Пружинки измерялись растяжением под действием силы 20g.
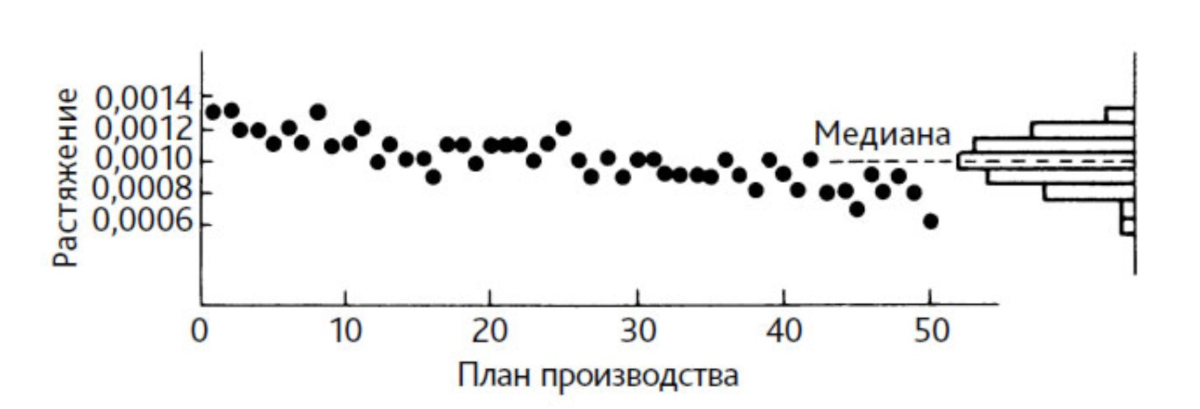
Рис. 2. Точечный график хода процесса с гистограммой распределения для 50 пружинок, испытанных в порядке их изготовления. Источник: [2] Эдвардс Деминг, книга "Выход из кризиса", стр. 224-225
Если не учитывать время изготовления, данные (Рисунок 2) образуют симметричное распределение, но если расположить их в порядке изготовления пружин, окажется, что распределение бесполезно. Например, распределение не сказало бы нам, в какой допуск могут попасть готовые пружинки. Причина в том, что здесь не существует идентифицируемого процесса.
Распределение выглядит довольно симметричным и не выходит за пределы допуска. Возникает искушение сделать вывод, что процесс находится в удовлетворительном состоянии. Однако значения растяжений, расположенные в порядке времени их изготовления, демонстрируют тренд в сторону уменьшения.
Что-то не так с процессом изготовления или с измерительным прибором. Любая попытка использовать распределение, показанное на рис. 2, бесполезна. Например, расчет стандартного отклонения для данного распределения не даст значения, которое можно использовать для предсказания. Оно ничего не говорит о процессе, поскольку он нестабилен.
Таким образом, мы получили очень важный урок – для анализа данных нужно посмотреть на них. Откладывайте точки в порядке производства изделий или в каком-то ином разумном порядке. Для некоторых проблем полезен простой точечный график.
Что, если кто-либо попытается использовать это распределение для расчета показателей воспроизводимости процесса? Он попадет в ловушку, из которой сложно выбраться. Процесс нестабилен. Ему вообще нельзя приписать никакой воспроизводимости.
Распределение (гистограмма) всего лишь демонстрирует накопленные данные работы процесса, ничего не говоря о его воспроизводимости. Процесс обладает воспроизводимостью, только если он стабилен. Воспроизводимость процесса достигается и подтверждается путем использования контрольной карты, но не самим распределением. Как мы уже видели, и простая карта хода процесса дает представление о воспроизводимости процесса".
В нашем программном обеспечении гистограмма распределения индивидуальных значений дополнена точечным графиком под гистограммой (Рисунок 3), который демонстрирует скрытую гистограммой информацию о процессе и является лучшей основой для стратификации данных.
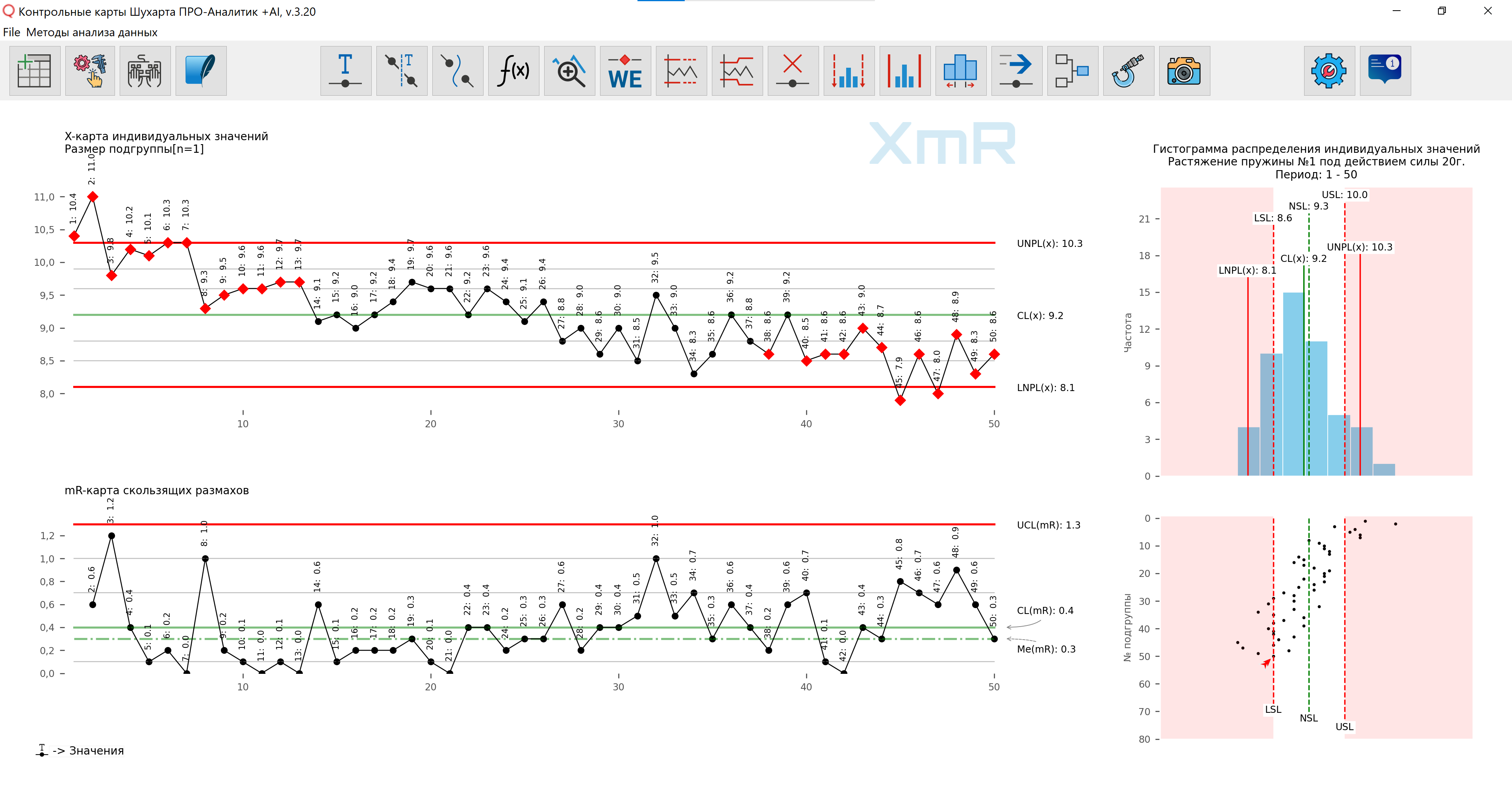
Рисунок 3. Рисунок подготовлен с использованием разработанного нами программного обеспечения .
Вы должны построить простые контрольные XmR-карты индивидуальных значений и скользящих размахов по данным, в хронологическом порядке выхода продукции, именно выхода, а не порядка измерения образцов .
Частая ошибка! Изделия поступающие для контроля передаются в общую кучу, а контролёры выбирают их по принципу, что удобно взять в первую очередь и в этом же порядке делают записи, хронологический порядок выхода продукции утрачивается.
Позаботьтесь о сборе этих данных заранее, производя отметку порядка выхода продукции каким-либо удобным способом. Более того, данные на гистограмме могут принадлежать различным типам источников вариабельности (станки, операторы, контролёры, партии сырья и т. д.) и источникам вариабельности внутри типа (например, станок-1, станок-2, станок-3). Хотя контрольные карты Шухарта (Shewhart control chart) хорошо справляются с анализом данных из смеси источников вариабельности, при использовании информации о доступных для учета источниках вариабельности (построение контрольных карт в разрезе источников вариабельности) вы получите значительно больше информации о процессе и как следствие будете иметь больше возможностей для его совершенствования. Опять же позаботьтесь о сборе этих данных заранее. И займитесь процедурами обеспечивающими прослеживаемость данных, это значительно облегчит выявление причинно-следственных связей.
На следующем уровне можно заняться анализом выхода процесса с помощью XbarR-карты средних и размахов подгрупп.
Так, для контрольной XbarR-карты Шухарта потребуется рациональная группировка данных в подгруппы с учётом типа и источников вариабельности. Например, для анализа зависимости показателя от конкретных операторов, группировка данных в подгруппы должна обеспечивать непопадание данных от разных операторов в какую-либо одну подгруппу.
Часто руководители ссылаются на пресловутый "человеческий фактор", объясняя этим абсолютное большинство проблем предприятия. Конечно, все люди отличаются друг от друга - как может быть иначе?! Но хочу напомнить, что анализируя работу людей, вы наблюдаете результат взаимодействия различных сотрудников с построенной вашим же менеджментом системой, и влияние системы на выход процесса значительно выше личного вклада отдельно взятых сотрудников, если это не художники с собственными красками, кистями и холстом.
Для людей с пытливым умом.
Есть в использовании гистограмм еще одна ловушка (обобщение) — размер кармана гистограммы (ширина столбца) в который попадают индивидуальные значения. Может оказаться так, что измерение немного отличающееся от попавшего в правый карман, попадает в левый. Происходит тоже самое, что с изделиями попадающими в поле допуска и за его пределы, смотрите определение Функции потерь качества Тагути . Я адаптировал подход Тагути для этого случая. Итак, внутри одного кармана гистограммы все индивидуальные значения добавляют равные частоты, увеличивающие высоту столбца. Если же значения немного выходят за границы кармана, они попадают в правый или левый карман соответственно. Но различия между значениями попадающими в один карман значительно больше чем у значений разместившихся у общей границы в соседних карманах. Поэтому гистограмма является полезным, но обобщающим инструментом, а тот, кто сравнивает соседние столбцы может быть легко введен в заблуждение. Более того, размер столбцов гистограммы значительно зависит от размера кармана гистограммы, вы можете легко убедиться в этом построив гистограммы с разным размером карманов для одного и того же ряда данных. Сделать эти простые эксперименты с дискретными данными поможет функция нашего программного обеспечения установка пользовательского размера кармана гистограммы , а для непрерывных значений функция: Масштабирование графика гистограммы по оси X и Y .
Индексы воспроизводимости Cp, Cpk
Рассчитывать индексы воспроизводимости Cp и Cpk для непредсказуемых процессов - бессмысленно, непредсказуемые процессы не воспроизводимы по определению.
Даже для процессов, находящихся в статистически управляемом состоянии, индексы воспроизводимости должные использоваться только в паре Cp, Cpk, иначе вы легко будете введены в заблуждение каждым из них. Понимание практического смысла индексов воспроизводимости, без дополнительной графического представления в виде гистограммы, сопряжено с лишней когнитивной нагрузкой на аналитика и тех кому он их пытается представить.
Индекс жизненного пространства (Cp) не говорит, где находится процесс относительно полей допуска, внутри или даже целиком за границами допуска. Индексы жизненного пространства Cp на рисунках 3 и 4 имеют одинаковые значения.
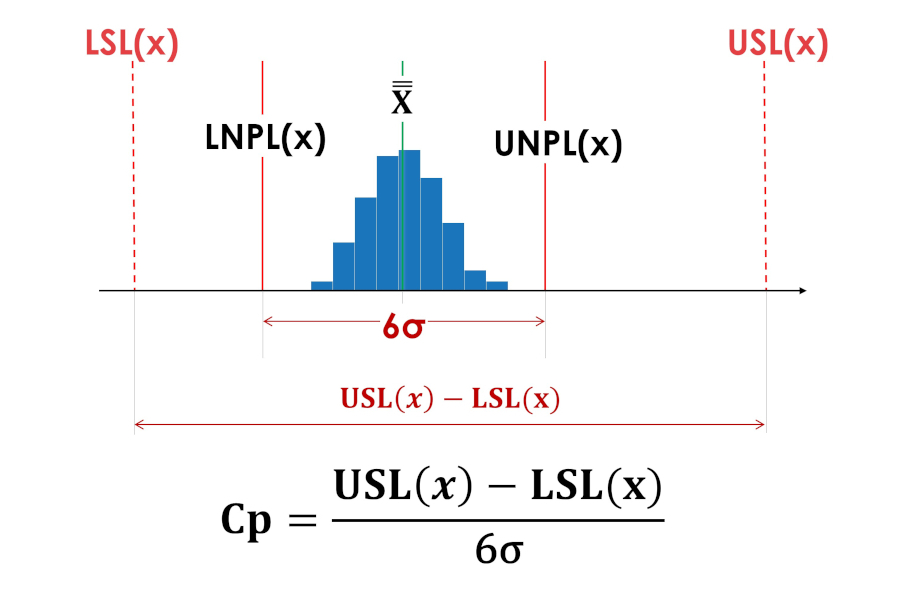
Рис. 3. Индексы фактической воспроизводимости процесса Cp (индекс жизненного пространства процесса). LSL(x) - Нижняя граница допуска; USL(x) - Верхняя граница допуска; LNPL(x) - Нижняя естественная граница процесса; X - Среднее средних процесса; UNPL(x) - Верхняя естественная граница процесса.
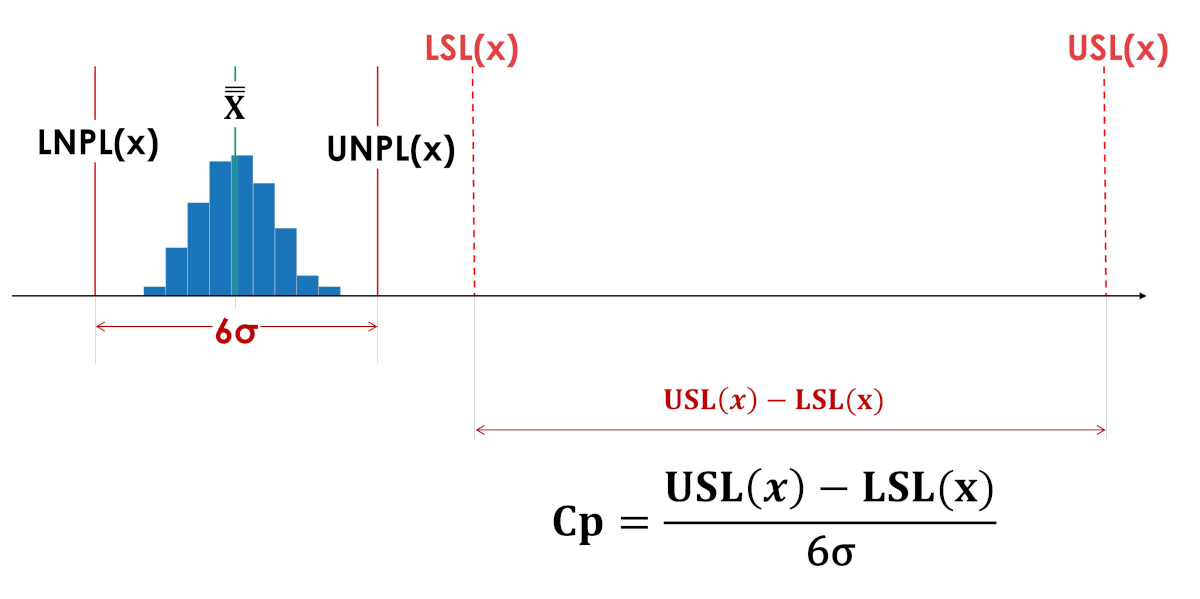
Рис. 4. Процесс искусственно смещён за границы поля допуска.
Индекс центрированности Cpk не даёт представления о стороне смещения от центра поля допуска, а следовательно, скрывает важную для улучшения процесса информацию, и не имеет смысла, если номинал не совпадает с центром поля допуска (несимметричные поля допусков).
Индексы центрированности Cpk на рисунках 5 и 6 имеют одинаковые значения.
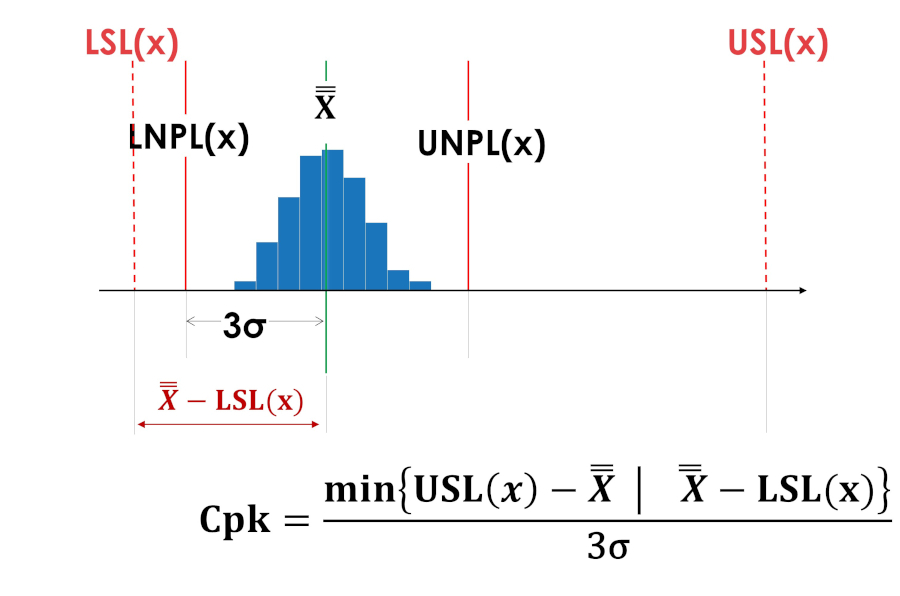
Рис. 5. Индекс центрированности Cpk процесса смещённого к нижней границе поля допуска.
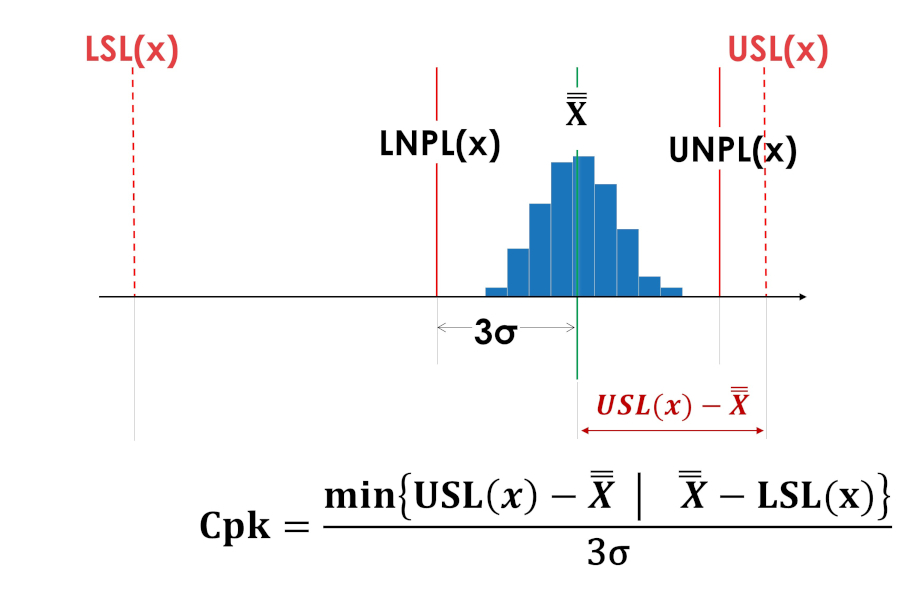
Рис. 6. Индекс центрированности Cpk процесса смещённого к верхней границе поля допуска.
И опять, гораздо больше полезной информации о процессе и о том, что необходимо делать для его улучшения, понятной всем, представляют простые графические методы: контрольные карты Шухарта, гистограмма распределения и простой точечный график контролируемых значений дополненный границами поля допуска.
Например, представьте, что вам сообщили следующие значения индексов воспроизводимости: Cp=2,6; Cpk=0,9 вместо демонстрации графиков, представленных на рисунке 7. Какую информацию легче и быстрее воспринимать? Какая форма передачи информации даёт более полное представление о процессе?
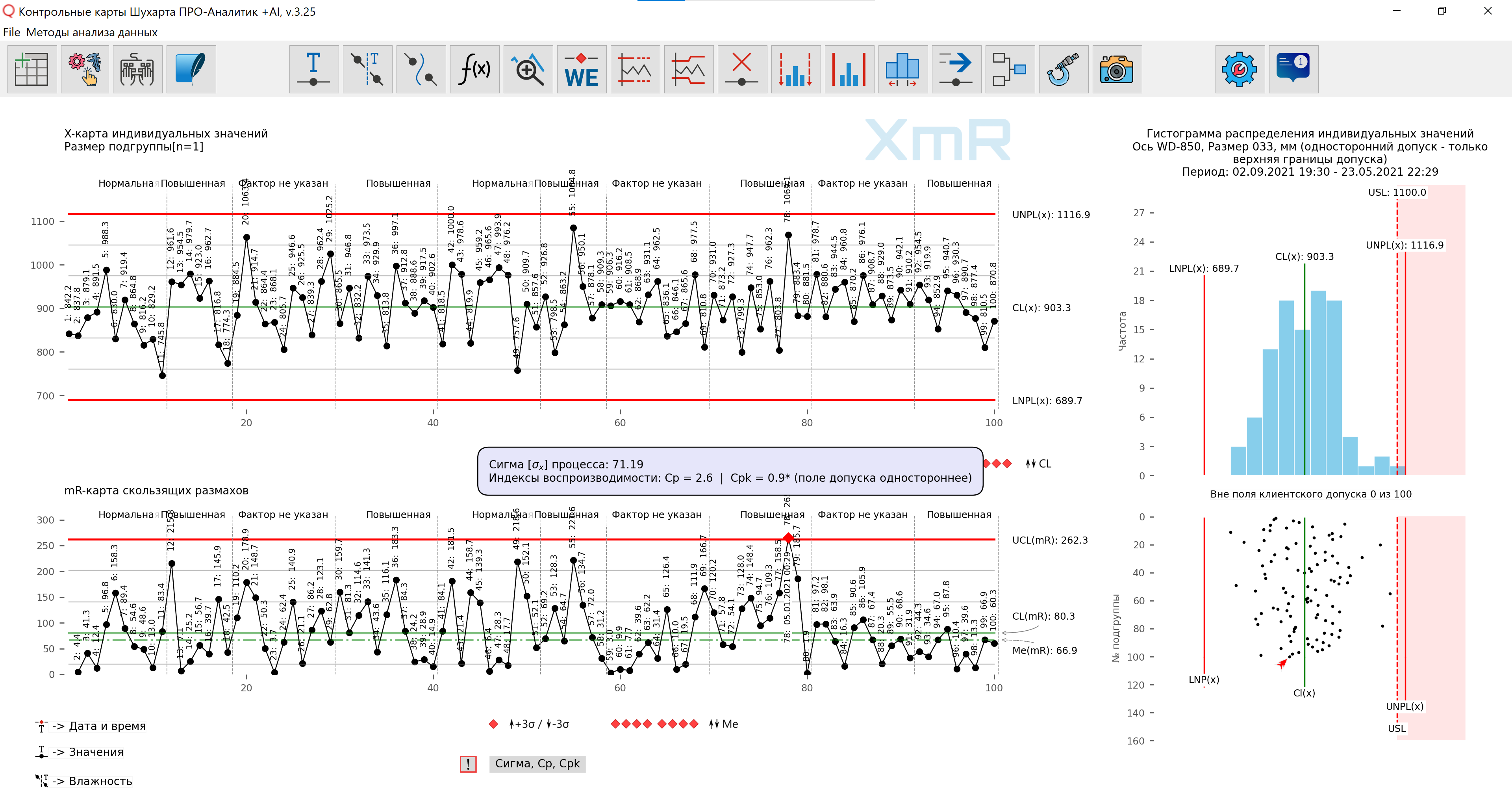
Рис. 7. Какую информацию легче и быстрее воспринимать? Какая форма передачи информации даёт более полное представление о процессе?