Контрольные карты для альтернативных данных (атрибутов, подсчётов) p-карта, np-карта, C-карта и u-карта или одна XmR-карта индивидуальных значений?
"Сложность использования p-карт, np-карт, C-карт или u-карт состоит в том, что трудно определить, подходят ли для данных биномиальные или пуассоновские модели".
Мы представляем перевод статьи Дональда Уилера: "А как насчет p-карты? Когда следует использовать контрольные карты p-карту, np-карту, C-карту и u-карту для альтернативных данных (подсчётов)?" / Donald J. Wheeler, Article: "What About p-Charts? When should we use the specialty charts p-chart, the np-chart, the c-chart, and the u-chart for count data?" [31]
Перевод и примечания: научный директор Центра AQT Григорьев С. П .
Бесплатный доступ к статьям нисколько не уменьшает ценности изложенных в них материалов.
Содержание
Все контрольные карты на основе данных для подсчётов являются картами для дискретных значений. Независимо от того, работаем ли мы с количеством или долями, мы получаем одно значение за период времени и хотим построить точку на графике каждый раз, когда мы получаем значение. Именно поэтому были разработаны четыре специальные контрольные карты для данных, основанных на подсчётах, ещё до того, как был обнаружен подход к построению контрольных XmR-карт индивидуальных значений и скользящих размахов. Это четыре вида контрольных карт р-карта, np-карта, C-карта, и u-карта. В этой статье задаётся вопрос, когда стоит использовать эти и другие специальные контрольные карты с данными, основанными на подсчётах.
Первая из этих специальных контрольных карт, p-карта (p-chart), была создана Вальтером Шухартом в 1924 году. В то время идея использования двухточечного скользящего размаха для измерения дисперсии набора отдельных значений ещё не возникла (У. Дж. Дженнет предложил эту идею в 1942 году). Итак, проблема, с которой столкнулся Шухарт, заключалась в том, как создать диаграмму поведения процесса для дискретных значений на основе подсчетов. Несмотря на то, что он мог построить данные в виде текущей записи, и хотя он мог использовать среднее значение в качестве центральной линии для этой текущей записи, препятствием было, как измерить дисперсию, чтобы отфильтровать обычные вариации. С дискретными значениями он не видел возможности, как использовать вариацию внутри подгруппы, но он знал, что лучше не пытаться использовать глобальную статистику стандартного отклонения, которая будет завышена любым имеющимся исключительным отклонением в имеющихся данных. Поэтому он решил использовать теоретические контрольные границы, основанные на вероятностной модели.
Классические вероятностные модели для простых данных подсчётов являются биномиальными и пуассоновскими, и Шухарт знал, что обе эти модели имеют параметр дисперсии, который является функцией их параметра местоположения. Это означало, что оценка среднего, полученная из данных, может также использоваться для оценки дисперсии. Таким образом, с помощью одной статистики местоположения он мог оценить как центральную линию, так и расстояние в три сигмы.
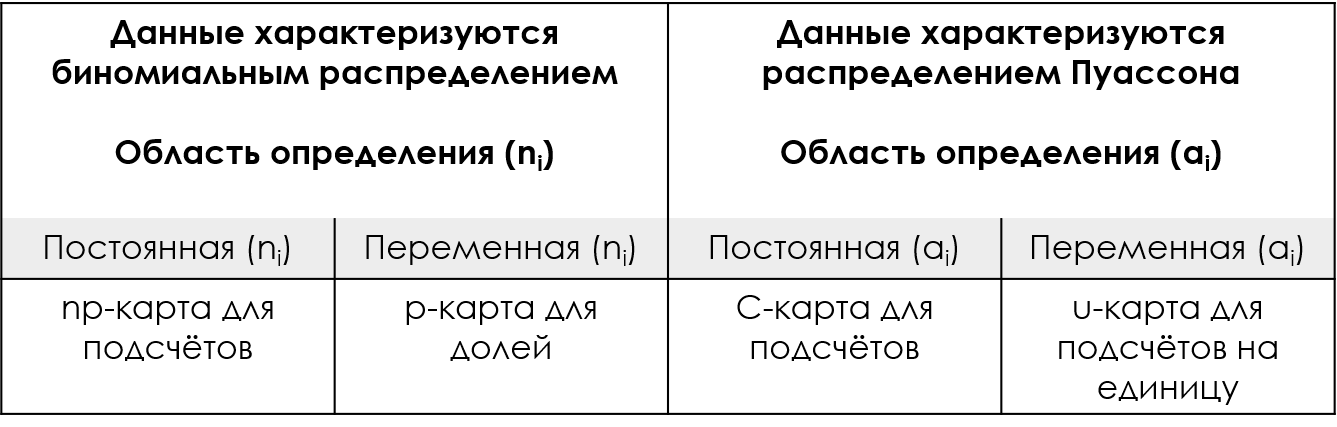
Рисунок 1: Специальные контрольные карты Шухарта для данных подсчётов.
Это двойное использование среднего значения для характеристики как местоположения, так и дисперсии означает, что p-карта, np-карта, C-карта, и u-карта имеют контрольные границы, которые основаны на теоретической связи между средним и дисперсией.
Следовательно можно сказать, что все специальные контрольные карты используют теоретические контрольные границы. Если подсчёты можно разумно смоделировать либо с помощью биномиального распределения, либо с помощью распределения Пуассона, то для карт дискретных значений могут быть получены соответствующие контрольные границы.
За последние годы многие учебники и стандарты забыли, что предположение о биномиальной модели или модели Пуассона является первичным условием для использования этих специальных контрольных карт. Это проблема, так как существует множество типов данных на основе подсчётов, которые не могут быть охарактеризованы ни как биномиальным, ни как Пуассоновским распределениями. При размещении таких данных на p-карте, np-карте, C-карте, и u-карте полученные теоретические контрольные границы будут неверны.
Так что же нам делать? Проблема с теоретическими контрольными границами заключается в предположении, что мы знаем точное соотношение между центральной линией и расстоянием в три сигмы. Решение состоит в том, чтобы получить отдельную оценку дисперсии, что и делает XmR-карта: в то время как среднее будет характеризовать местоположение и служить центральной линией для X-карты индивидуальных значений, средний скользящий размах mR-карты будет характеризовать дисперсию и служить основой для вычисление расстояния трех сигм для X-карты.
Таким образом, основное различие между специальными контрольными картами для подсчётов и XmR-картой индивидуальных значений и скользящих размахов заключается в способе вычисления расстояния трех сигм. Контрольные p-карта, np-карта, C-карта и u-карта будут иметь ту же текущую запись и, по сути, те же центральные линии, что и X-карта. Но когда дело доходит до вычисления трех-сигмовых контрольных границ, специальные контрольные карты используют предполагаемую теоретическую взаимосвязь для вычисления теоретических значений, в то время как XmR-карта фактически измеряет вариацию, присутствующую в данных, и строит эмпирические контрольные границы.
Чтобы сравнить специальные контрольные карты с XmR-картой, мы будем использовать три примера. Первый из них будет использовать данные, показанные на рисунке 2. Эти значения поступают из бухгалтерии, которая отслеживает, сколько счетов закрыто «вовремя» ежемесячно. Показанные подсчёты представляют собой ежемесячное количество закрытий, которые были завершены вовремя на 35 закрытий (равную область определения).
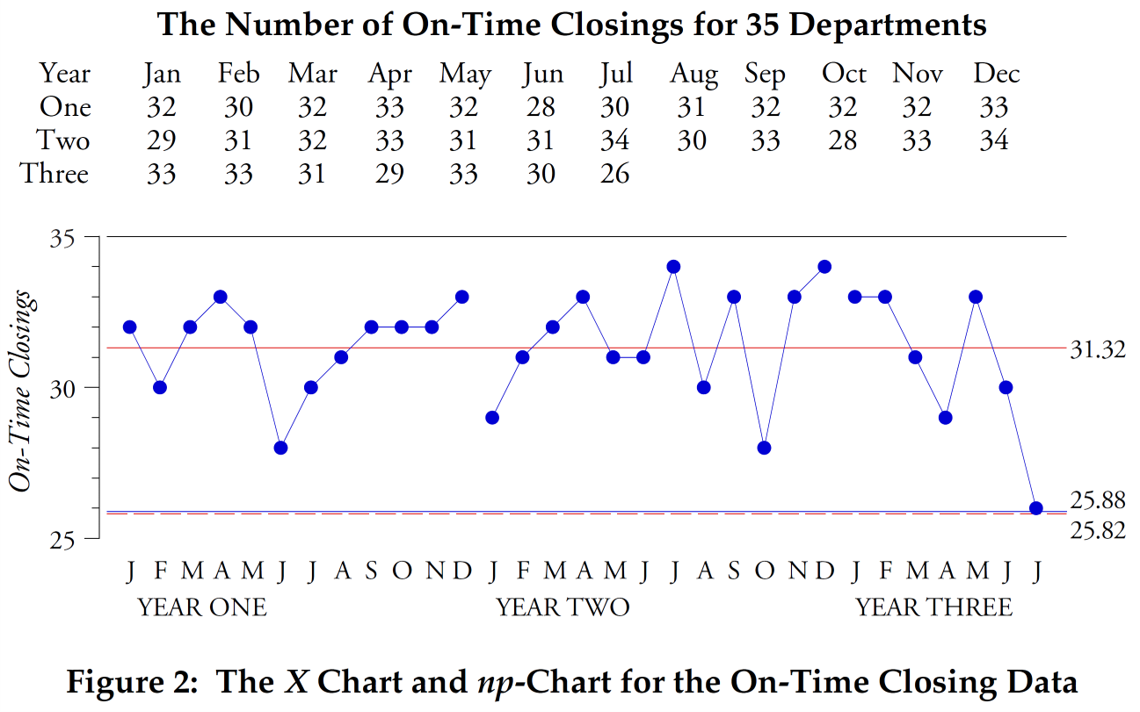
Рис. 2: Х-карта и np-карта ежемесячного количества вовремя закрытых счетов из каждых 35 счетов.
Красные пунктирные линии - верхняя и нижняя контрольные границы для X-карты, синие для p-карты.
Здесь вычисления как для np-карты, так и для X-карты индивидуальных значений дают практически одинаковые контрольные границы (верхняя контрольная граница со значением 36,8 не показана, поскольку она превышает максимальное значение 35 своевременных закрытий). Здесь два подхода по существу идентичны, потому что эти подсчёты, по-видимому, соответствующим образом моделируются биномиальным распределением. Если вы достаточно опытны, чтобы определить, когда это произойдет, тогда вы узнаете, когда np-карта будет работать, и сможете успешно её использовать. С другой стороны, если вы недостаточно опытны, чтобы знать, когда подходит биномиальная модель, вы все равно можете использовать XmR-карту. Как можно увидеть здесь, когда np-карта работала бы, эмпирические контрольные границы X-карты будут идентичны теоретическим контрольным границам np-карты, и вы ничего не потеряете, используя XmR-карту вместо np-карты.
В нашем следующем примере мы будем использовать своевременные поставки для завода. Данные для процента своевременных поставок по месяцам за два года показаны на рисунке 3 вместе с X-картой индивидуальных значений и p-картой для этих данных.
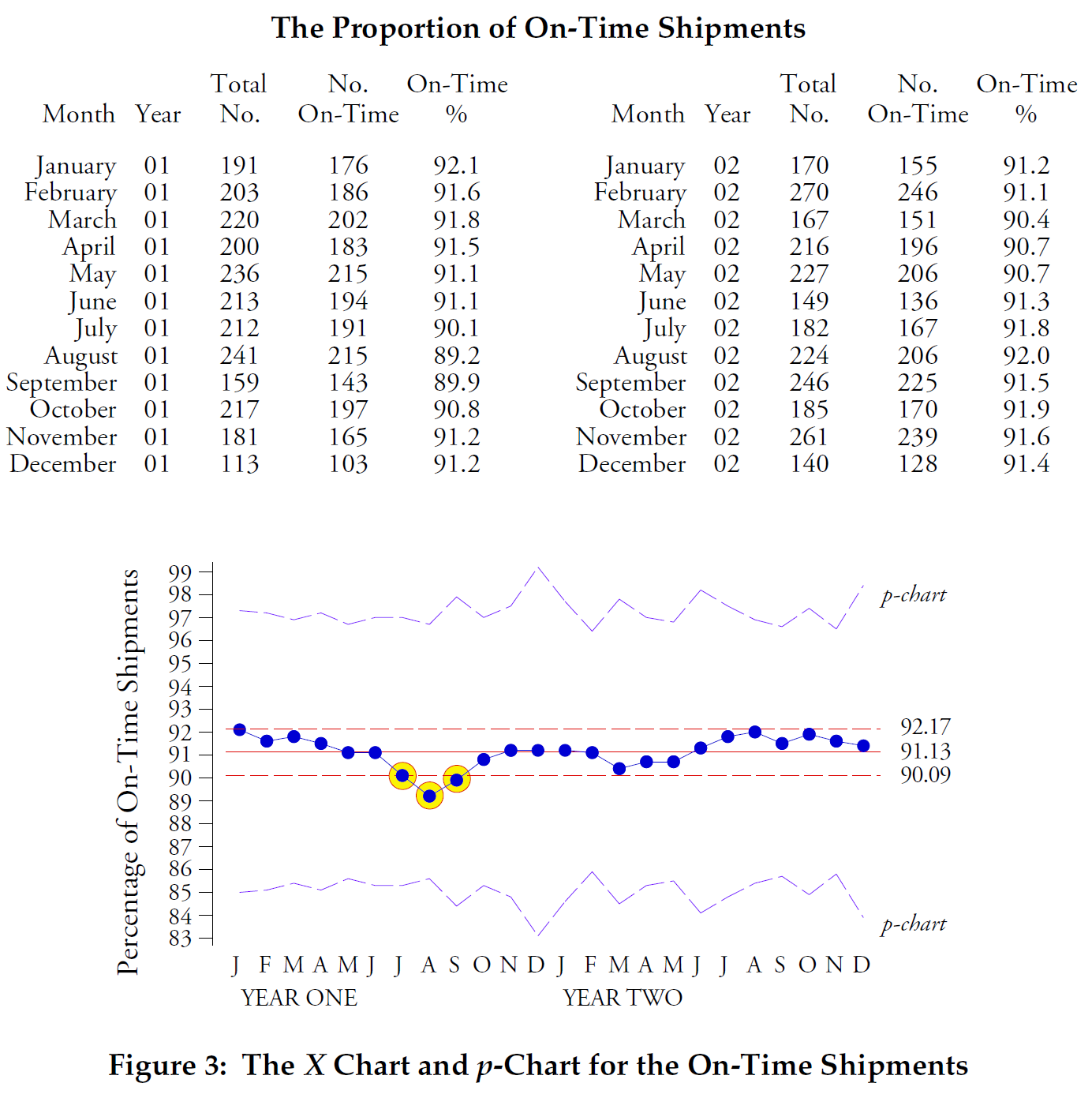
Рисунок 3: Х-карта и p-карта для процента своевременных поставок по месяцам за два года.
На X-карте показан процесс с тремя точками на нижней контрольной границе или ниже. Контрольные границы переменной ширины p-карты в пять раз шире, чем контрольные границы X-карты, найденные с использованием скользящих размахов. Никакие точки не выходят за эти контрольные границы p-карты. Это несоответствие между двумя наборами контрольных границ указывает на то, что данные на рисунке 3 не удовлетворяют биномиальным условиям. В частности, вероятность того, что отгрузка будет доставлена вовремя, не одинакова для всех отправлений в любой конкретный месяц. Поскольку биномиальная модель не подходит для этих данных, теоретические контрольные границы p-карты неверны. Однако эмпирические контрольные границы XmR-карты, которые не зависят от соответствия конкретной вероятностной модели, верны.
В нашем последнем сравнении будут использоваться данные из рисунка 4. Здесь у нас есть процент поступающих грузов для одного завода по сборке электроники, которые были отправлены с использованием авиаперевозок. Две точки выходят за контрольные границы переменной ширины p-карты , но ни одна точка не выходит за контрольные границы X-карты.
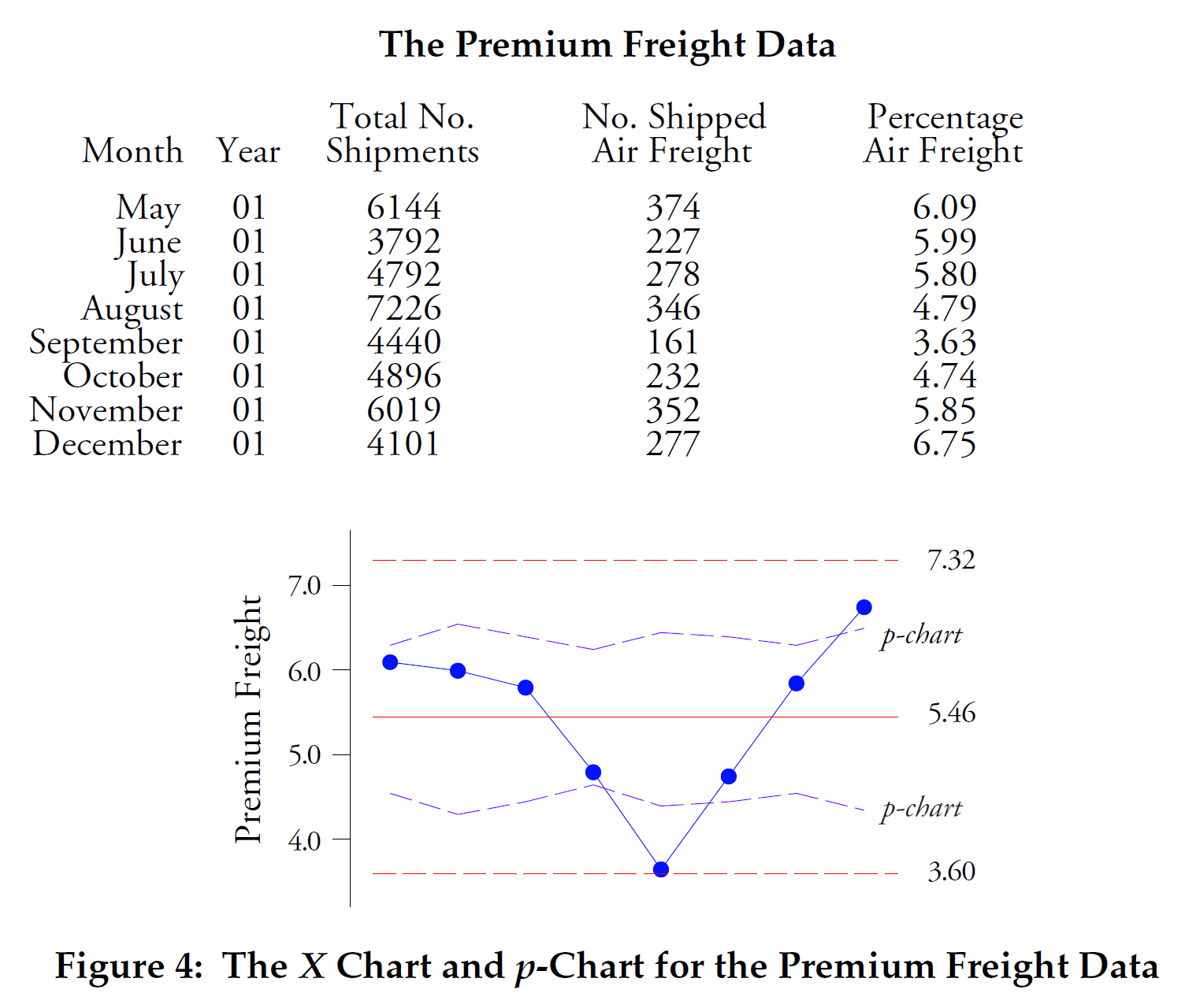
Рисунок 4: X-карта индивидуальных значений и p-карта для процента отгрузок с использованием авиаперевозок.
На рисунке 4 типично то, что происходит, когда область определения (англ., "area of opportunity") для подсчета предметов становится чрезмерно большой. Биномиальная модель требует, чтобы все элементы в любой заданный период времени имели одинаковые шансы обладать подсчитываемым атрибутом. Здесь это требование не выполняется. С тысячами отправлений каждый месяц вероятность того, что партия будет отправлена по воздуху, не одинакова для всех отправлений. Таким образом, биномиальная модель не подходит, а теоретические контрольные границы p-карты, которые зависят от биномиальной модели, неверны. Контрольные границы X-карты, которые здесь вдвое шире, чем контрольные границы p-карты, правильно характеризуют как расположение, так и разброс этих данных и являются правильными контрольными границами для использования.
Таким образом, сложность использования p-карт, np-карт, C-карт или u-карт состоит в том, что трудно определить, подходят ли для данных биномиальные или пуассоновские модели. Как видно на рисунках 3 и 4, если вы упустите первичное условия для специальных контрольных карт, вы рискуете совершить серьезную ошибку на практике. Вот почему вам следует избегать использования специальных контрольных карт, если вы не знаете, как оценить соответствие данных этим вероятностным моделям.
В отличие от использования теоретических моделей, которые могут быть или не быть правильными, XmR-карта предоставляет нам эмпирические контрольные границы, которые фактически основаны на вариации, присутствующей в данных. Это означает, что вы можете использовать XmR-карту с данными на основе подсчётов в любое время. Поскольку p-карта, np-карта, C-карта и u-карта являются частными случаями диаграммы для дискретных значений, XmR-карта будет имитировать эти специальные диаграммы, когда они подходят, и будет отличаться от них, когда они ошибаются.
В случае специальных контрольных карт, имеющих контрольные границы переменной ширины, XmR-ката будет имитировать контрольные границы, основанные на средней области определения контрольных карт для подсчётов. Кроме того, при проведении этих сравнений я предпочитаю иметь не менее 24 подсчётов в базовый период.
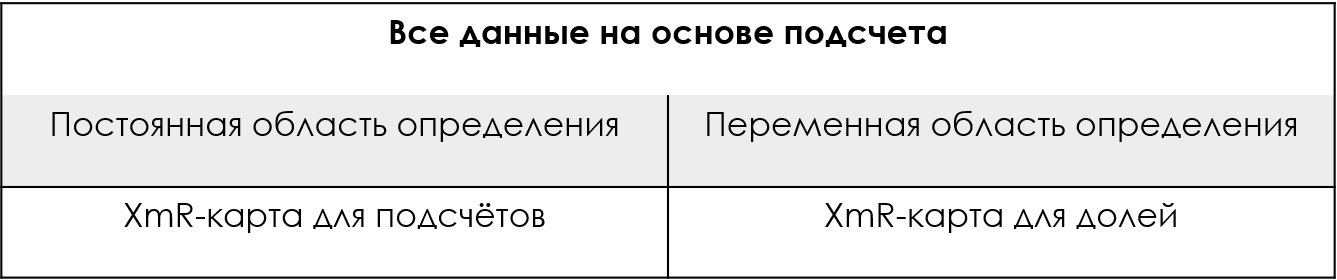
Рисунок 5: Подход без допущений для данных на основе подсчётов.
Таким образом, если у вас нет ученых степеней в области статистики или если вам просто трудно определить, можно ли характеризовать ваши подсчеты биномиальным или пуассоновским распределением, вы все равно можете проверить свой выбор специальной карты для своих данных на основе подсчётов путем сравнения теоретических контрольных границ с эмпирическими контрольными границами XmR-карты. Если эмпирические контрольные границы примерно такие же, как теоретические, тогда вероятностная модель работает. Если эмпирические контрольные границы не соответствуют теоретическим контрольным границам, то вероятностная модель неверна.
Вы всегда можете быть уверены, что у вас получены правильные контрольные границы для ваших данных, основанных на подсчётах, если вы используете с самого начала XmR-карту. Эмпирический подход всегда будет правильным.
Примечание (С. Григорьев)
В своей книге "Статистическое управление процессами. Оптимизация бизнеса с использованием контрольных карт Шухарта" Дональд Уилер так определяет еще одно условие необходимое для минимизации влияния дискретности данных подсчётов на эмпирические контрольные границы XmR-карты индивидуальных значений:
"XmR-карту для дискретных данных можно построить во всех случаях, когда среднее значение подсчета больше единицы. Если же оно больше двух, то влияние дискретности на контрольные границы будет ничтожным.
Поскольку редко имеет смысл использование дискретных величин, когда можно получить результаты измерений, использование атрибутов, в общем, ограничивается такими ситуациями, когда можно подсчитывать «ляпы». Однако определение «ляпа» обычно представляет огромную трудность.
Главная трудность в определении «ляпа» — это проблема операциональных определений ".
Таким образом, если у вас среднее значение подсчётов на область определения меньше двух, вы можете легко нейтрализовать эту проблему увеличив область определения для получения среднего значения подсчётов до значения равного или более 3 (трём), что особенно актуально для событий с распределением Пуассона (подсчитываются дефекты, а не дефектные изделия и можно подсчитать только дефекты, но ни в коем случае не число "недефектов").
Например
Если у вас среднее число подсчётов дефектов на область определения равную одному квадратному метру ткани равно 1 (единице), вы можете использовать область определения из трёх метров квадратных, получив среднее число дефектов на новую область определения равное 3 (трём) метрам квадратным. Используйте ту область определения, которую легко сможете выделять для проверки (испытания), например, для рулона полотна ткани шириной 1,2 метра можно использовать область определения в 3 погонных метра.
Формула расчёта необходимой минимальной области определения:
Если среднее подсчётов исторических данных < 3, тогда
новая минимальная область определения получается умножением текущей области определения на коэффициент (k):
k = 3/среднее значение подсчётов исторических данных;
минимальная новая область определения = k × текущая область определения.
Выберите удобную для контроля область определения (=) или (>) полученной минимальной новой области определения.
Для биномиальных величин (да/нет, дефектное/недефектное, не вовремя/вовремя), можно использовать XmR-карту для значений положительных, а не отрицательных исходов, как это реализовано в примерах 1 (рисунок 2) и 2 (рисунок 3) этой статьи Дональда Уилера. Влияние дискретности данных биномиальных моделей на XmR-карту индивидуальных значений подчиняется тем же правилам, что и для пуассоновских моделей, придерживайтесь среднего значения подсчётов исходов (да/нет) не менее 3 (трёх).
Внимание!
Если области определения различны, вы не можете сравнивать числа подсчётов без приведения их в доли от соответствующих областей определения. Если всё же вам сложно интерпретировать доли, вы можете привести полученные значения подсчётов к одной области определения, как в примере 1 этой статьи Д. Уилера на примере контрольной карты вовремя закрытых счетов. Для этого вы можете воспользоваться формулой, показанной ниже.
Искомое:
x i - приведённое к постоянной области определения число подсчётов.

"Все доли — дроби, но не все дроби — доли. Дробь можно считать долей тогда, когда знаменатель будет описывать область определения для значений числителя".
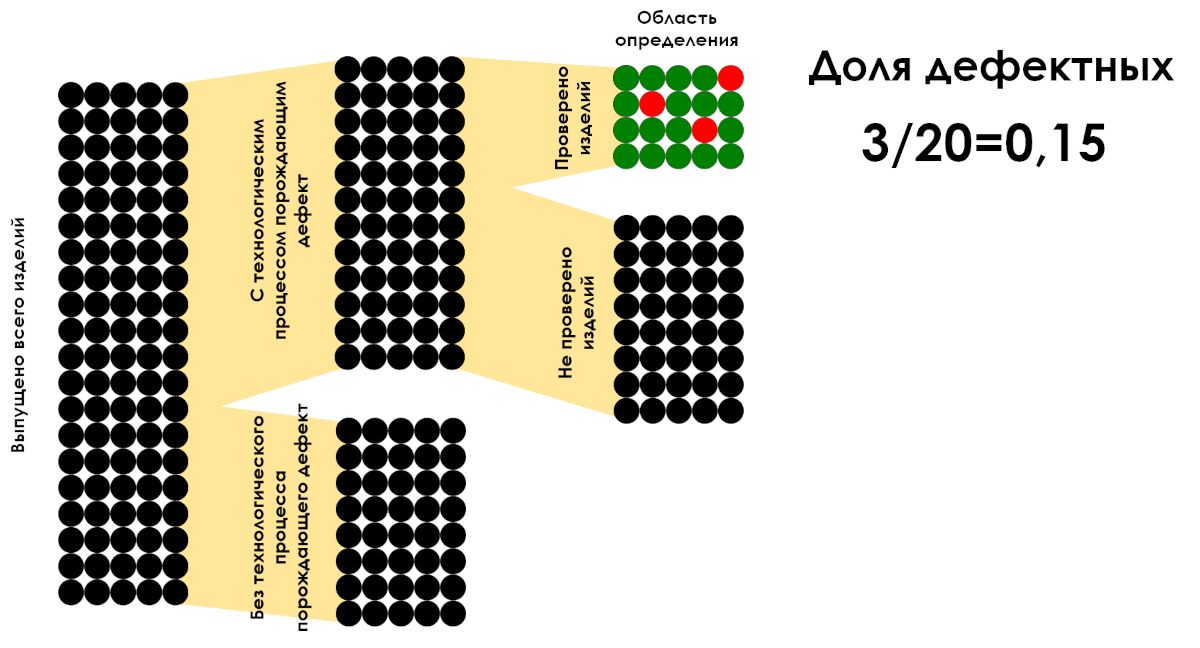
Рисунок 6: Пример расчёта доли дефектных изделий на область определения. Только отношение 3/20 является долей.
Вы должны позаботиться о следовании всем рекомендациям этой статьи ещё на шаге планирования сбора данных. В абсолютном большинстве случаев, если данные не представляют результат 100%-го контроля, любые манипуляции с имеющимися историческими данными по увеличению области определения с использованием математики, исказят картину происходящего.