Рациональная группировка данных для эффективного использования контрольных XbarR-карт средних и размахов подгрупп
Источник: Статья, любезно предоставленная нам Доктором Дональдом Уилером (англ.): [35] Рациональная группировка. Концептуальные основы диаграмм поведения процессов / Rational Subgrouping. The conceptual foundation of process behavior charts, Donald J. Wheeler.
Переводчик и научный редактор: Григорьев С. П.
Бесплатный доступ к статьям нисколько не уменьшает ценности изложенных в них материалов.
Важный аспект эффективного использования контрольных карт — их способность отвечать на правильные вопросы. Для этого способ распределения данных по подгруппам должен соответствовать структуре данных. Обычно это означает, что в каждую подгруппу следует группировать данные из некоторой «малой области» — пространства, времени, партии продукции, чтобы внутри подгруппы данные были как можно более однородными. Акцент на минимизации вариации внутри подгрупп проистекает из того факта, что именно эта вариация используется при расчете контрольных пределов. Контрольные пределы зависят от среднего размаха, который, в свою очередь, зависит от индивидуальных групповых размахов, отражающих вариацию внутри подгрупп. Именно вариация внутри подгрупп используется для установления контрольных пределов, которые определяют, какая вариация допустима между подгруппами.
Вопрос, который ставит контрольная карта средних: «А не варьируют ли групповые средние больше, чем должны, если опираться на внутригрупповую вариацию?» Иначе говоря: «При допущенной вариабельности внутри подгрупп определимы ли различия между групповыми средними?»
Карта размахов подгрупп спрашивает: «Устойчива ли вариация внутри подгрупп от подгруппы к подгруппе?» Или, иначе: «При допущенной средней вариации внутри подгрупп определимы ли различия вариаций в разных подгруппах?».
Разница в этих двух вопросах будет проиллюстрирована несколькими примерами.
Толщина листа
Виниловый лист шириной 30 дюймов (762 мм), используемый для изготовления обшивки панелей с мягкой подкладкой, был экструдирован под контролем автоматического контроллера процесса. В качестве устройства ввода для этого автоматического контроллера процесса использовался традиционный бета-сканер, измеряющий толщину винила. Инженер хотел изучить показания толщины вдоль одной дорожки, расположенной в 10 дюймах от левого края листа винила, поэтому он собрал все данные для этой дорожки и нанес их на контрольную XbarR-карту средних и размахов подгрупп, используя подгруппы размером четыре.
Используя подгруппу размером четыре, он гарантировал, что каждая подгруппа будет представлять около двух минут работы процесса. По его мнению, это позволило проявиться обычным изменениям (случайными вариациями, обусловленными общими причинами) в процессе экструзии в каждой подгруппе. Контрольная карта средних на рисунке 1 показывает, что автоматический контроллер регулировал процесс вверх и вниз циклами продолжительностью около 20 минут. Хотя средняя толщина составляла 48,5 мм, она могла составлять 49,5 мм за пять или шесть минут, прежде чем через шесть минут упала до 47 мм. Это изменение толщины повлияло на то, как винил будет нагреваться и растягиваться при вакуумном формовании. Это изменение толщины приводило к образованию отходов на следующем этапе, но в среднем винил был подходящей толщины!
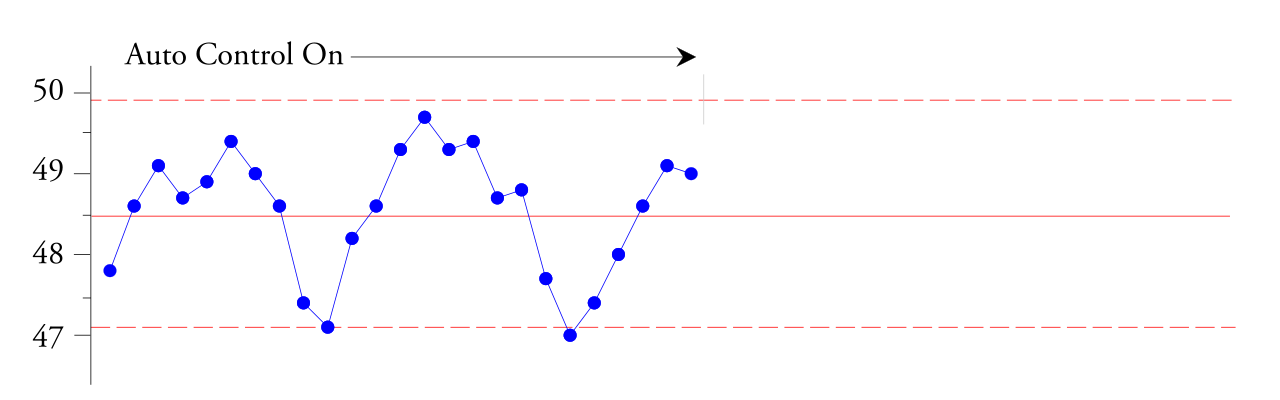
Рис. 1. Контрольная XbarR-карта средних подгрупп толщины виниловых листов при автоматическом контроле.
Точки внутри контрольных границ имеют тренд то вврех, то вниз, чтобы сказать нам, что этот автоматический контроллер процесса недостаточно демпфирован , не поддерживает хороший установившийся отклик и нуждается в помощи. По словам инженера, создавшего эту контрольную XbarR-карту, легко «распознать синусоидальную волну», которую мы наблюдаем. Исходя из наблюдаемого явления на рисунке 1, инженер выключил автоматический контроллер процесса. В течение следующего 45-минутного периода он получил новые значения, показанные справа на рисунке 2.
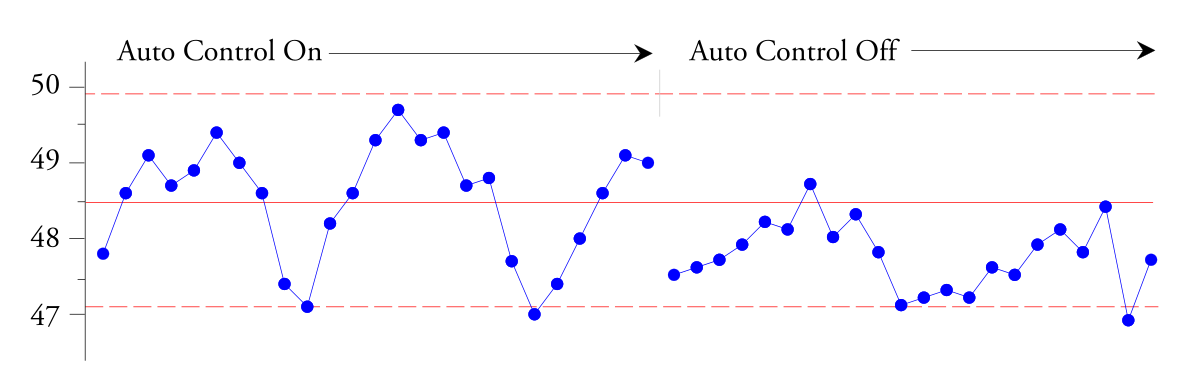
Рис. 2. Контрольная XbarR-карта средних подгрупп толщины виниловых листов (продолжение).
Это подтвердило, что примерно половина вариаций толщины листа происходила из-за автоматического контроллера процесса. Поскольку эти вариации приводят к появлению брака на выходе, этот автоматический контроллер процесса необходимо правильно настроить, чтобы исключить эти 20-минутные циклы. Обратите внимание, как путь от интерпретации графика к формулировке необходимого действия зависит как от контекста данных, так и от того, как эти данные организованы в подгруппы.
Время до максимального крутящего момента
Чтобы охарактеризовать свойства отверждения партий резиновой смеси, образец из каждой партии должен быть испытан в лаборатории. В этом тесте измеряется крутящий момент образца резины во время его отверждения. Результатом испытаний было время отверждения, необходимое для достижения максимального крутящего момента. Поскольку каждый из трёх операторов производил пять партий резины за каждую смену, лаборатория решила использовать пять дневных значений для каждого оператора в качестве их подгрупп. Это привело к появлению одной подгруппы в смену, причем вариация внутри подгруппы была вариацией от партии к партии для каждого оператора, а вариация между подгруппами была вариацией от оператора к оператору и изо дня в день. Поскольку все операторы производили один продукт с использованием одной резиновой мельницы, мы ожидали увидеть предсказуемый процесс при построении XbarR-карты средних и размахов подгрупп.
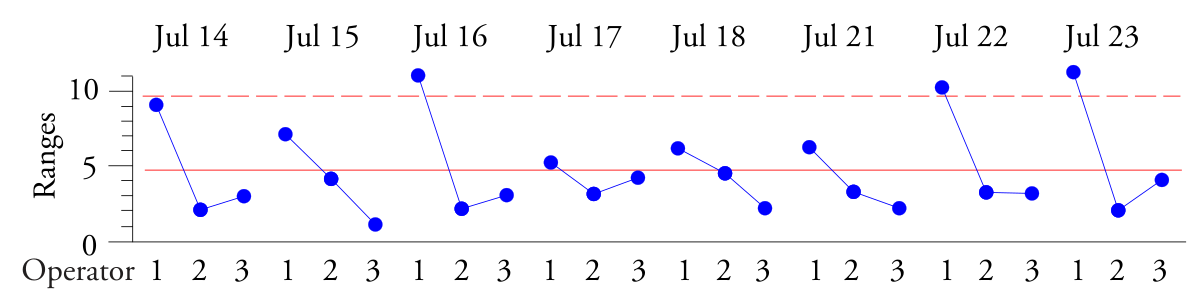
Рис. 3. Контрольная R-карта размахов подгрупп для времени до максимального крутящего момента.
R-карта групповых размахов показывает повторяющуюся модель «максимум-минимум-минимум». Партии, произведенные Оператором 1, демонстрируют большую вариацию, чем партии, произведенные Операторами 2 и 3. Хотя Оператор 1 был старшим оператором с 30-летним опытом, он не смешивал свои партии должным образом. Оказалось, что это произошло из-за того, что Оператор 1 терял зрение и не мог видеть достаточно хорошо для ручного смешивания.
Еще раз, ключ к интерпретации данных - организация данных на контрольной карте. Контрольная R-карта групповых размахов показывает отсутствие согласованности внутри подгрупп, а идентификация каждой подгруппы с помощью одного оператора позволяет нам понять схему, показанную на рисунке 3. Именно организация данных определяет, какие вопросы будут рассмотрены на контрольной XbarR-карте средних и размахов подгрупп. Изменения местоположения, происходящие между подгруппами, будут отображаться на X-карте средних значений подгрупп. Изменения в вариациях, которые происходят в разных подгруппах, будут отображаться на R-карте групповых размахов. В каждом случае именно вариации внутри подгрупп определяют критерий для обнаружения любых возникающих различий. Понимание этого - ключ к эффективному анализу данных наблюдений.
В первом примере, приведенном выше, это была последовательная схема, предлагающая простой эксперимент по отключению автоматического контроллера процесса. Во втором примере это был подход, который соответствовал структуре данных, что привело к открытию слепого оператора. В обоих случаях к открытиям привела интерпретация диаграмм в их контексте. Готовность к подобному мышлению, которое соответствуют способу сбора и построения данных, нельзя запрограммировать. Это зависит от того, кто потратит время и приложит усилия, чтобы посмотреть на графики и подумать над ними. Это всегда было и всегда будет неотъемлемой частью эффективного использования контрольных карт поведения процессов.
Для некоторых наборов данных рациональное разделение на подгруппы будет достаточно простым. Однако для некоторых наборов данных может быть несколько возможных способов разбивки данных на подгруппы. Следующий пример попадает в эту категорию.
Шарнирные головки, изготовленные методом литья под давлением
Литье под давлением используется для изготовления шарнирного соединения по четыре штуки за раз. На момент сбора этих данных этот метод изготовления представлял собой изменения как в материалах, так и в технологиях. Поэтому перед запуском в серийное производство требовалось пройти сертификацию процесса. Дэйв, руководитель, решил использовать контрольные карты поведения процессов, чтобы оценить этот процесс до сертификации.
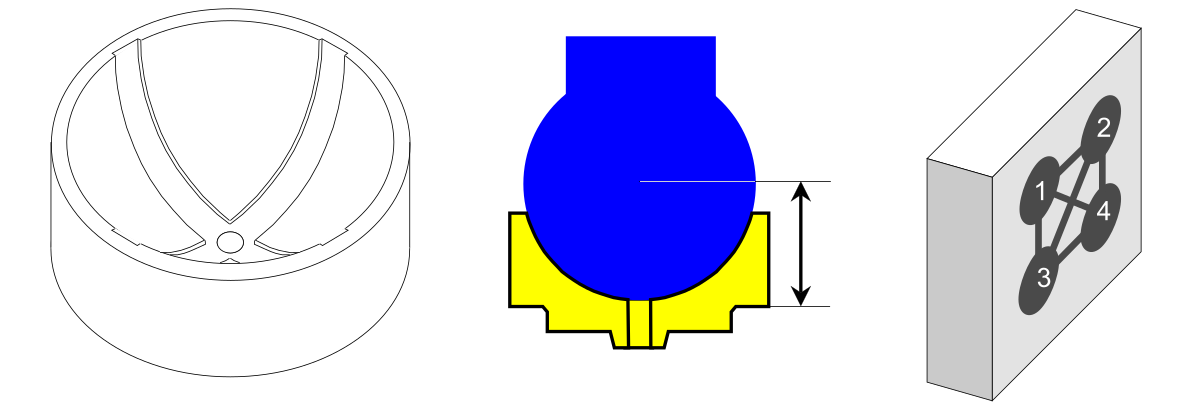
Рис. 4. Шаровая муфта, размер по толщине и пресс-форма, имеющая 4 полости.
Поскольку была только одна пресс-форма, в процессе сертификации участвовал только один пресс и только один оператор. Данные представляли собой эффективную толщину шаровой муфты, измеренную в сотых долях миллиметра. Поскольку одна сторона шаровой муфты была вогнутой, для измерения этой толщины пришлось разработать и изготовить специальный калибр. Измерения калибром показывают толщину, превышающую 12,00 миллиметров. Четыре раза в день Дэйв подходил к прессу и собирал детали, произведенные пятью последовательными циклами пресса. Поскольку каждый цикл производил четыре детали (по одной из каждой полости), ему приходилось измерять 20 деталей каждые два часа. Соблюдая осторожность, Дэйв отслеживал цикл и полость, из которой вышла каждая деталь.
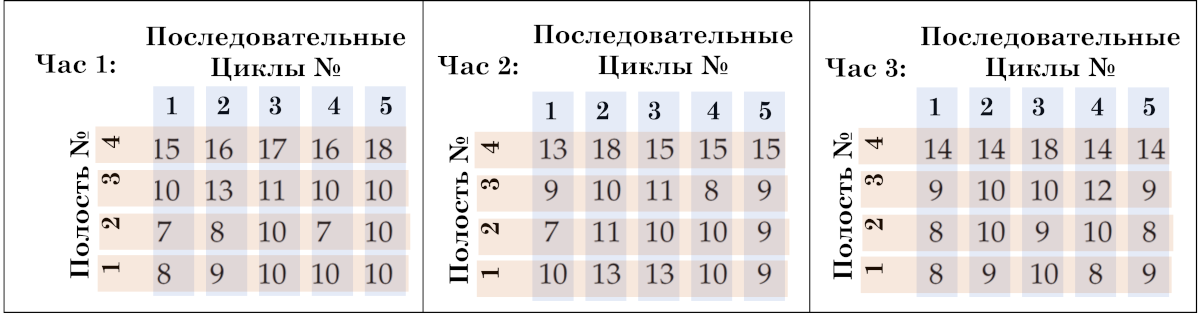
Рис. 5. Структура почасовых данных о толщине шаровой муфты. Hour (Час), Consecutive Cecles (Последовательные циклы), Cavity (Полость пресс-формы).
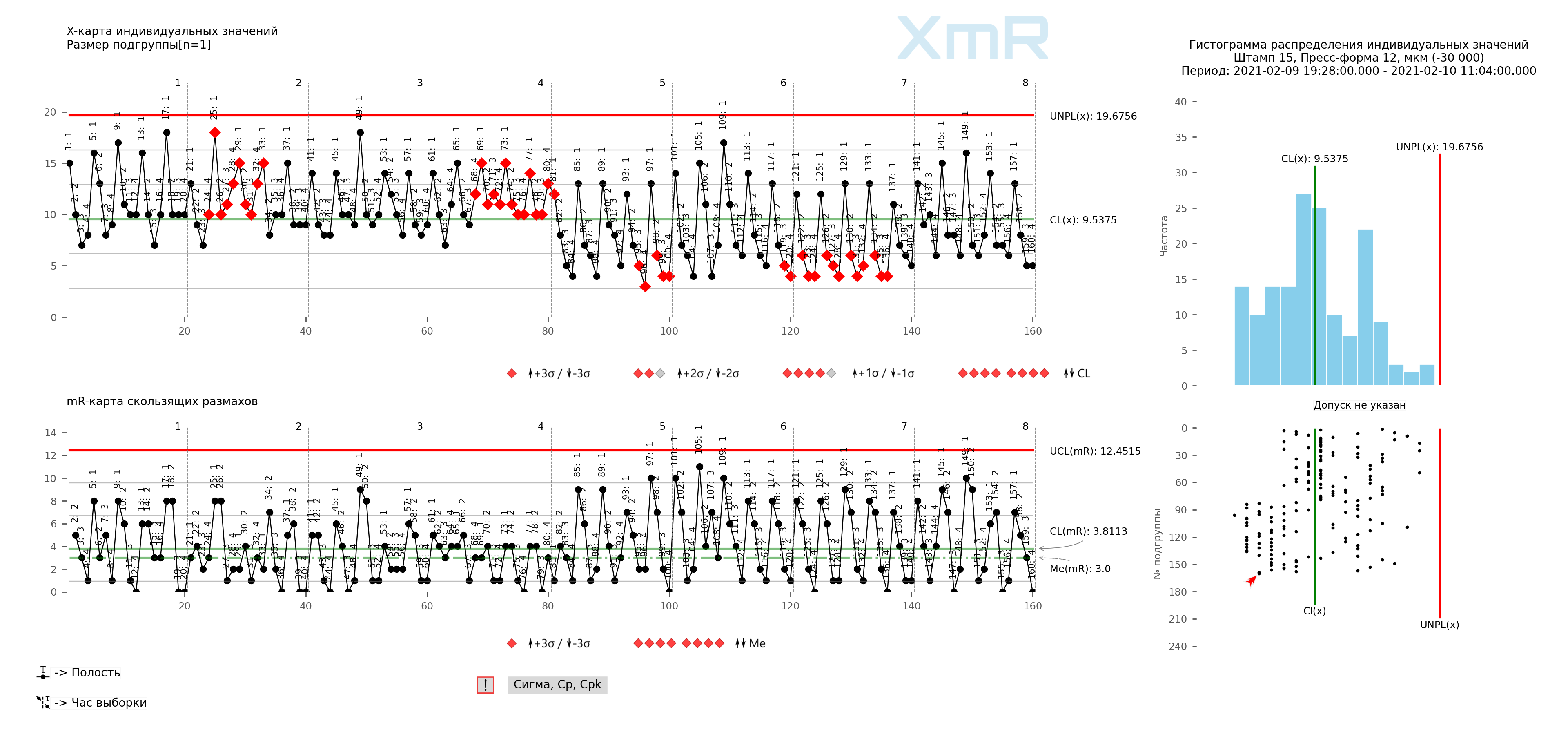
Рис. 6. Структура почасовых данных о толщине шаровой муфты, на карте хода процесса (XmR-карте индивидуальных значений и скользящих размахов). Вертикальные разделители: Час, подписи всех точек: Полость пресс-формы. Рисунок подготовлен с использованием разработанного нами «Контрольные карты Шухарта ПРО-Аналитик +AI (для Windows, Mac, Linux)» .
В этих данных есть три идентифицируемых источника вариации. Есть почасовая вариация, которая представлена различными наборами (блоками) из 20 значений на рисунке 5. Существует вариация от цикла к циклу, которая представлена различными столбцами на рисунке 5 (1, 2, 3, 4, 5). И есть вариация от полости к полости, которая представлена разными строками на рисунке 5 (1, 2, 3, 4).
Мы рассмотрим различные способы их группировки для контрольной XbarR-карты средних и размахов подгрупп, а также влияние каждой организации данных в подгруппы на интерпретацию контрольных карт. Для процедуры сертификации Дэйв собирал данные шесть дней. Для краткости мы будем использовать данные только за первые два дня.
Полный набор данных и первая организация в подгруппы показаны на рисунке 7. Каждый столбец из четырех значений используется для определения подгруппы, так что наши 160 значений организованы в 40 подгрупп размером n=4. Данные за разные часы (1, 2, 3 и т. д.) находятся в разных подгруппах. Когда вы меняете часы, вы меняете подгруппы. Следовательно, в этой первой организации данных в подгруппы можно сказать, что почасовые различия (а также ежедневные различия) проявляются между подгруппами. Здесь XbaR-карта средних задаст следующие вопросы:
Вопрос № 1: Есть ли заметные различия между часами или днями?
На рисунке 8 данные из разных циклов (1, 2, 2, 4, 5) находятся в разных подгруппах. Когда вы меняете циклы, вы меняете подгруппы. Следовательно, можно сказать, что межцикловые различия проявляются между подгруппами в этой первой организации этих данных. Здесь карта средних подгрупп также задаст следующий вопрос:
Вопрос № 2: Есть ли заметные различия между циклами?
На рисунке 8 данные из разных полостей (1, 2, 3, 4) находятся в одной подгруппе. Когда вы меняете полости, вам не нужно менять подгруппы. Следовательно, можно сказать, что различия между полостями проявляются внутри подгрупп в этой первой организации этих данных. Итак, здесь карта групповых размахов задаст следующий вопрос:
Вопрос № 3: Согласованы ли различия между полостями?

Рис. 7. Первый способ организации данных в подгруппы.
Среднее значение - 9,54; средний размах составляет 7,63, что приводит к контрольным пределам, показанным на рисунке 8. Делая разрыв линии графика, мы упрощаем его чтение, давая нашим глазам привязку к каждому часу отдельно. Хотя ни одна точка не выходит за установленные пределы, на графике средних значений подгрупп есть четкий сигнал. Когда 20 из 20 средних значений находятся выше центральной линии, за которыми следуют 19 из 20 ниже центральной линии, существует реальная разница между первым и вторым днями. Также на карте размахов подгрупп может отображаться дневная разница. Итак, мы отвечаем на вопрос № 1 (Есть ли заметные различия между часами или днями?) однозначно «да», мы отвечаем на вопрос № 2 (Есть ли заметные различия между циклами?) отрицательно и отвечаем на вопрос № 3 (Согласованы ли различия между полостями?) вероятно «нет».
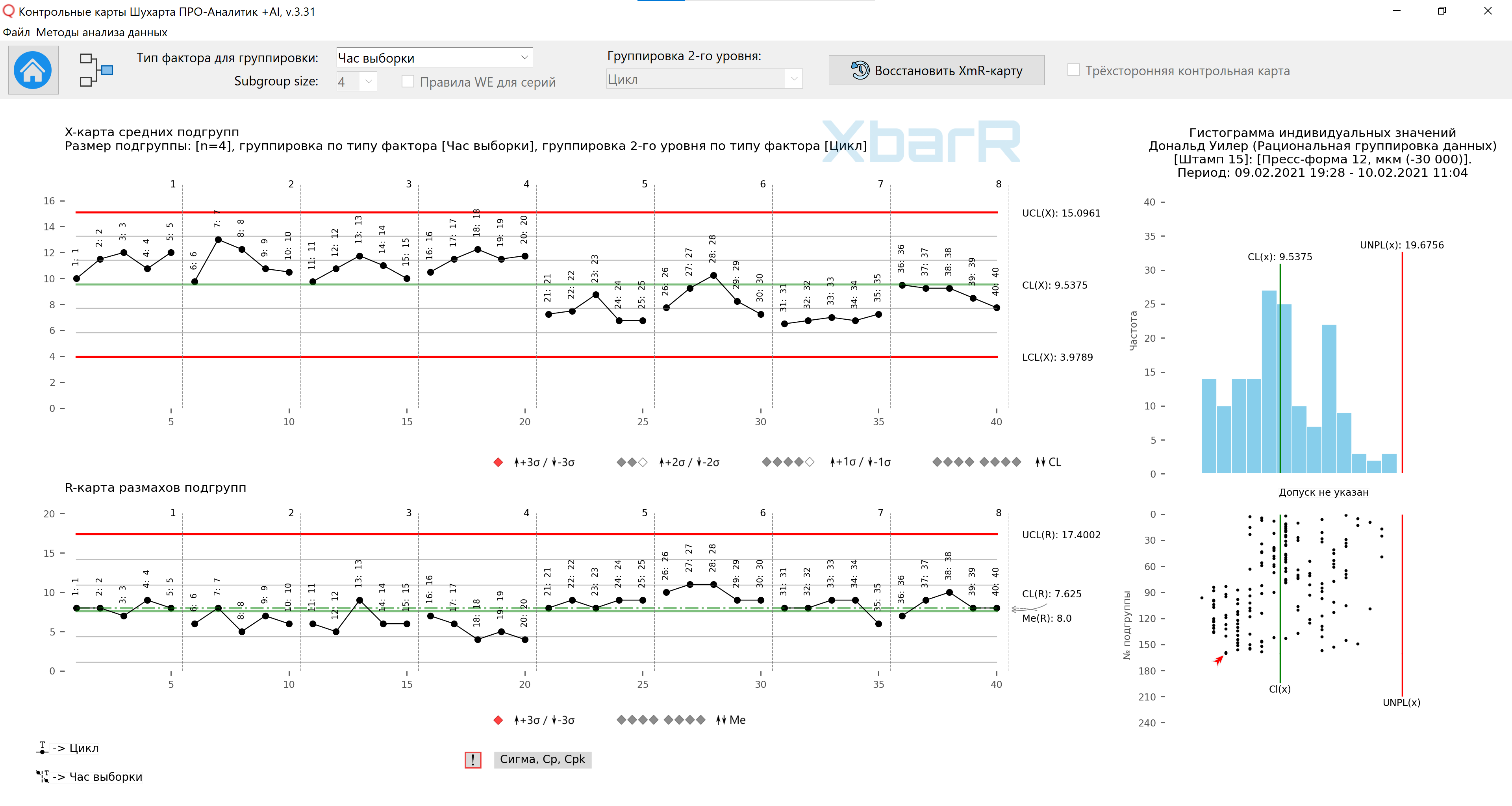
Рис. 8. Карта средних и размахов подгрупп для первого способа организации данных в подгруппах. Вертикальные линии разделения серий со значениями от 1 до 8 - Часы отбора образцов, подписи всех точек - № Цикла. Рисунок подготовлен с использованием разработанного нами «Контрольные карты Шухарта ПРО-Аналитик +AI (для Windows, Mac, Linux)» с использованием уникальной функции автоматизации рациональной группировки данных для построения XbarR-карты средних и размахов подгрупп по выбранному типу источников вариаций (столбцу с факторами) и размеру подгрупп.
Второй способ организации данных в подгруппах
Второй способ организации этих данных показан на рисунке 9. Там каждая строка из пяти значений используется для определения подгруппы, так что мы получаем 32 подгруппы размером n=5. Здесь данные из разных часов (1:, 2:, 3: и т. д.) находятся в разных подгруппах. Когда вы меняете часы, вы меняете подгруппы. Следовательно, во второй организации можно сказать, что почасовые (и ежедневные) различия проявляются между подгруппами. Здесь карта средних подгрупп задаст следующий вопрос:
Вопрос № 4: Есть ли заметные различия между часами или днями?
На рисунке 9 данные из разных циклов (1, 2, 3, 4, 5) находятся в одной подгруппе. Когда вы меняете циклы, вам не нужно менять подгруппы. Таким образом, можно сказать, что межцикловые различия проявляются внутри подгрупп во второй организации этих данных. Здесь диаграмма групповых размахов задаст следующий вопрос:
Вопрос № 5: Последовательны ли различия между циклами?
На рисунке 9 данные разные полости (1, 2, 3, 4) находятся в разных подгруппах. Когда вы меняете полости, вы меняете подгруппы. Таким образом, можно сказать, что различия между полостями проявляются между подгруппами во второй организации этих данных. Здесь график средних подгрупп также задает следующий вопрос:
Вопрос № 6: Есть ли заметные различия между полостями?
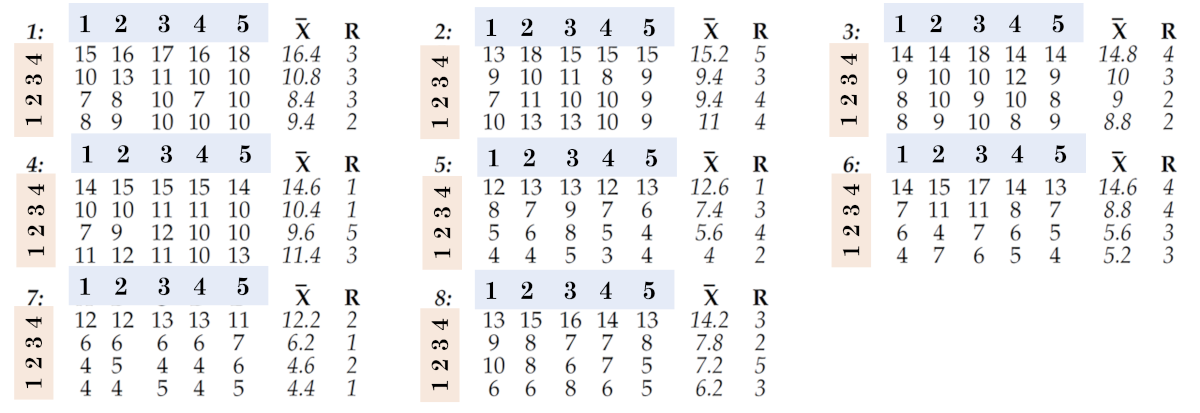
Рис. 9. Второй способ организации данных в подгруппы.
Среднее значение - 9,54; средний размах составляет 2,84, что приводит к контрольным пределам, показанным на рисунке 10. Поскольку 20 из 32 наших средних значений выходят за контрольные пределы, у нас есть множество сигналов для интерпретации. Есть заметные различия между двумя днями и есть заметные различия между четырьмя полостями. Более того, изменение от цикла к циклу, по-видимому, согласовано от подгруппы к подгруппе (R-карта размахов подгрупп).
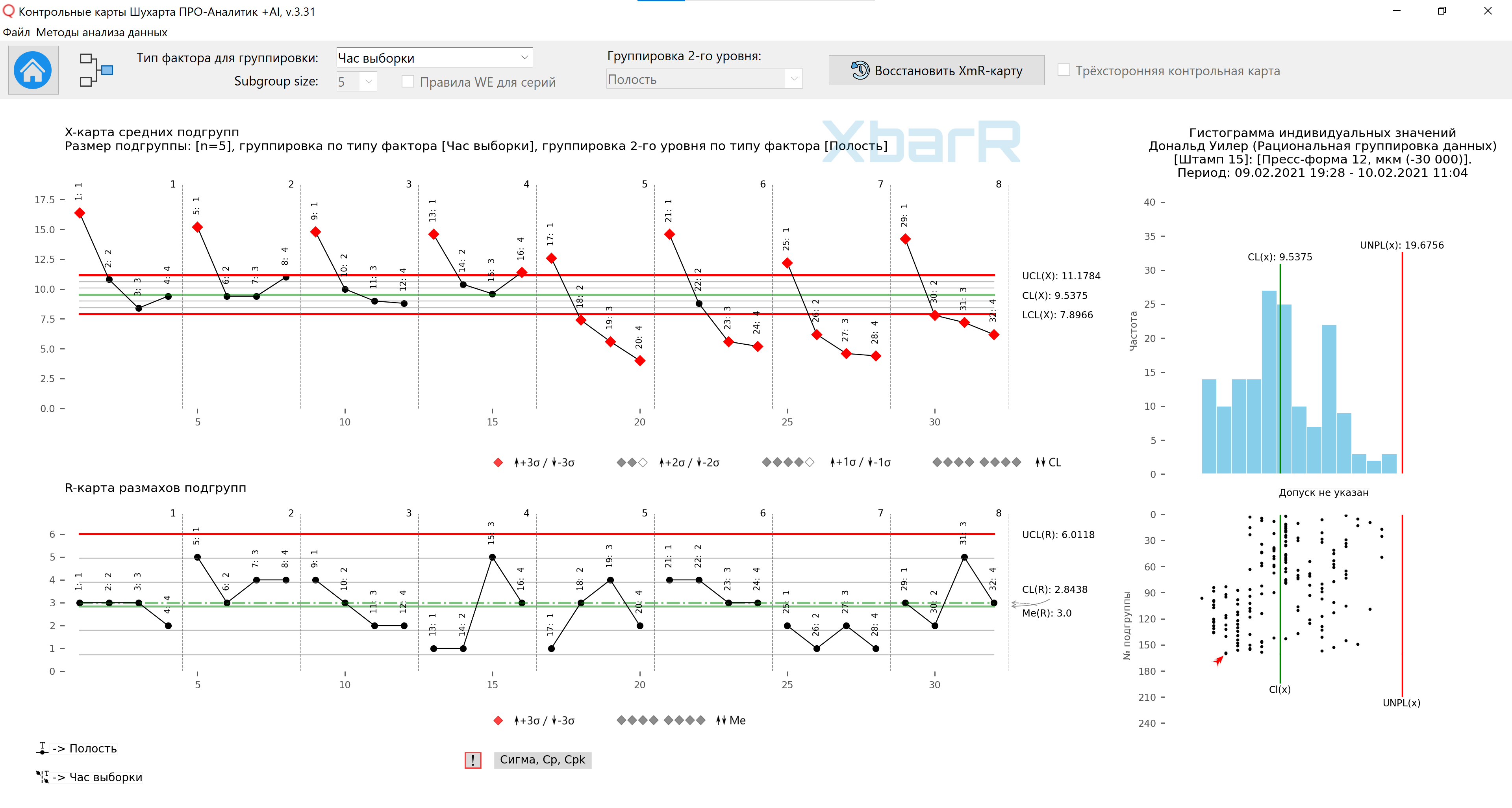
Рис. 10. Диаграмма средних и размахов подгрупп для второго способа организации данных в подгруппах. Вертикальные линии разделения серий со значениями от 1 до 8 - часы отбора образцов. Подписи всех точек - № Полости. Рисунок подготовлен с использованием разработанного нами «Контрольные карты Шухарта ПРО-Аналитик +AI (для Windows, Mac, Linux)» с использованием уникальной функции автоматизации рациональной группировки данных для построения XbarR-карты средних и размахов подгрупп по выбранному типу источников вариаций (столбцу с факторами) и размеру подгрупп.
Обе вышеперечисленные организации данных в подгруппах технически правильны, но на практике они не одинаковы, потому что они не задают одни и те же вопросы к данным. Чтобы понять эту разницу, рассмотрите вопрос № 3 и вопрос № 6.
Результатом первой организации данных стал вопрос № 3: «Согласованы ли различия между полостями?». Карта групповых размахов на рисунке 8 ответила на этот вопрос утвердительно. Различия между полостями постоянны.
Результатом второй организации стал вопрос № 6, в котором спрашивалось: «Есть ли заметные различия между полостями?». Карта средних подгрупп на рисунке 10 ответила на этот вопрос утвердительно. Между четырьмя полостями есть заметные различия. В полости (1) получаются более толстые детали, чем в других полостях.
Пока вы не поймете разницу между Вопросом № 3 и Вопросом № 6, и пока вы не поймете, как использовать это различие для получения ответов на интересующие вас вопросы, вы не поймете рациональное разделение на подгруппы. Это навык, требующий практики и размышлений. Вы можете потренироваться, ответив на вопросы в следующем разделе.
Третий способ организации данных в подгруппы
Дэйв не использовал ни одну из предыдущих организаций данных в подгруппы. Вместо этого он использовал способ организации данных в подгруппы, показанный на рисунке 11, для своего сертификационного теста. Мы снова используем каждую строку из пяти значений как подгруппу размера пять, поэтому подгруппы такие же, как и во второй организации, но теперь мы организуем их по-другому. Вместо одной диаграммы с 32 подгруппами у нас будет отдельная диаграмма для каждой полости.
На рис. 10, фиксируя полость и цикл, меняете ли вы подгруппы от часа к часу?
Так можно ли найти почасовые различия внутри подгрупп или между подгруппами?
Итак, где будут проявляться почасовые различия: на карте размахов или карте средних значений подгрупп?
На рисунке 10 при фиксированных часах и полости меняете ли вы подгруппы при переходе от цикла к циклу?
Так можно ли найти различия между циклами внутри подгрупп или между подгруппами?
Итак, где будут проявляться межцикловые различия: на карте размахов или карте средних значений?
На рисунке 10, при фиксированных часах и циклах, меняете ли вы подгруппы при переходе от полости к полости?
Так где же можно найти различия между полостями?
Так где же проявятся различия между полостями?
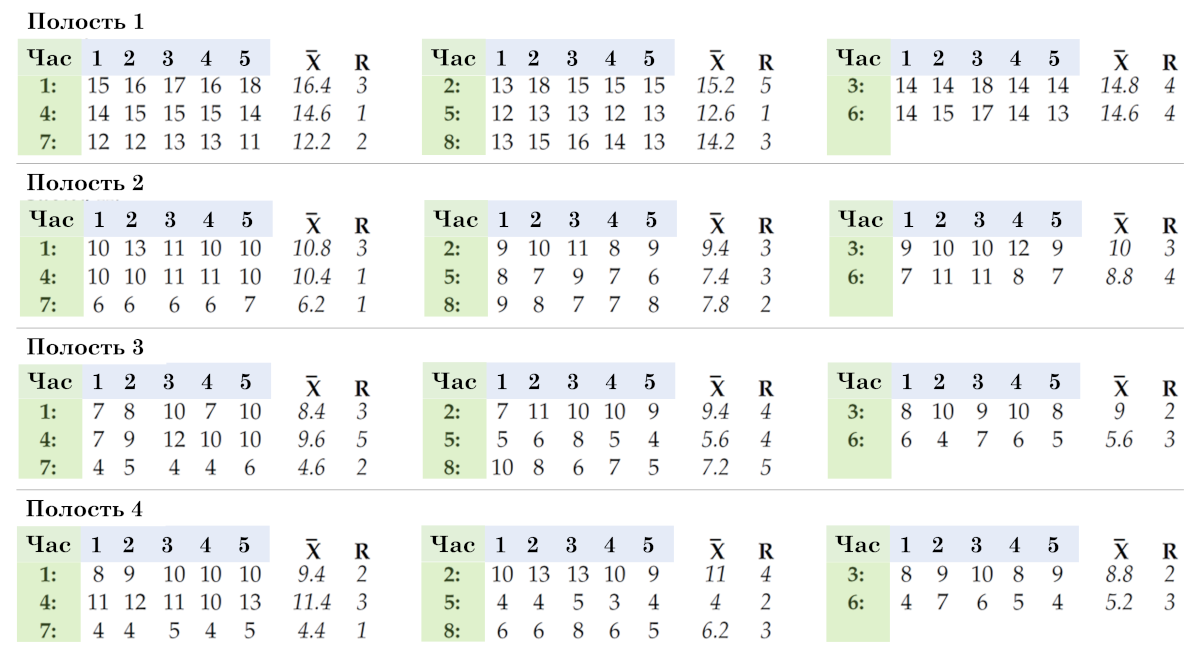
Рис. 11. Третий способ организации данных в подгруппы.
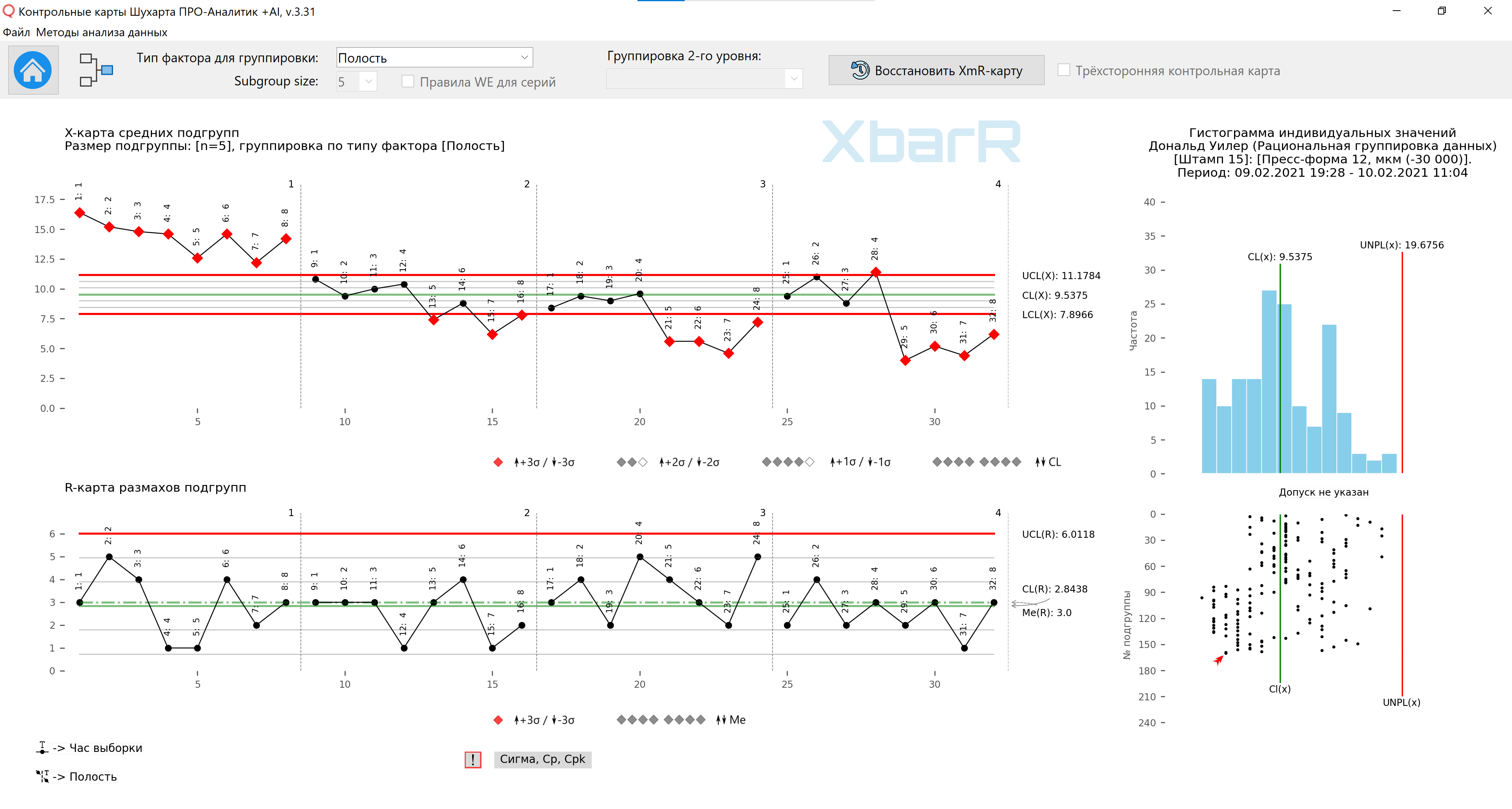
Рис. 12. Карта средних и размахов подгрупп для третьего способа организации данных в подгруппах. Вертикальные линии разделения серий со значениями от 1 до 4 - № Полостей. Подписи всех точек - Час выборки. Рисунок подготовлен с использованием разработанного нами «Контрольные карты Шухарта ПРО-Аналитик +AI (для Windows, Mac, Linux)» с использованием уникальной функции автоматизации рациональной группировки данных для построения XbarR-карты средних и размахов подгрупп по выбранному типу источников вариаций (столбцу с факторами) и размеру подгрупп.
Построив все четыре диаграммы в одном вертикальном масштабе, мы покажем различия между полостями. Очевидно, что полость (1) делает детали более толстыми, а полость (2) немного толще, чем полости (3) и (4). Основываясь на этих графиках, Дэйв знал, что ему нужно внести поправки в форму. Поскольку полости (3) и (4) были достаточно хорошо отцентрированы в пределах поля допуска, он попросил инструментальный цех разместить прокладки за полостями (1) и (2).
Какой источник отклонений обнаруживается на диаграммах размахов? Часы? Циклы? Полости?
Какой источник отклонений обнаруживается на картах средних значений? Часы? Циклы? Полости?
Так что же означают точки, выходящие за контрольные пределы на приведенных выше картах средних значений?
Если у вас возникли проблемы с предыдущими вопросами, возможно, вам придется прочитать эту статью еще раз.
Можно продолжить обработку данных контрольной карты с Рисунка 12 и с использование функции построения контрольных границ для отдельных серий разделить серии данных в области отдельных полостей по видимым признакам, получив подтверждение функционирования различных процессов до и после чистки изложницы.
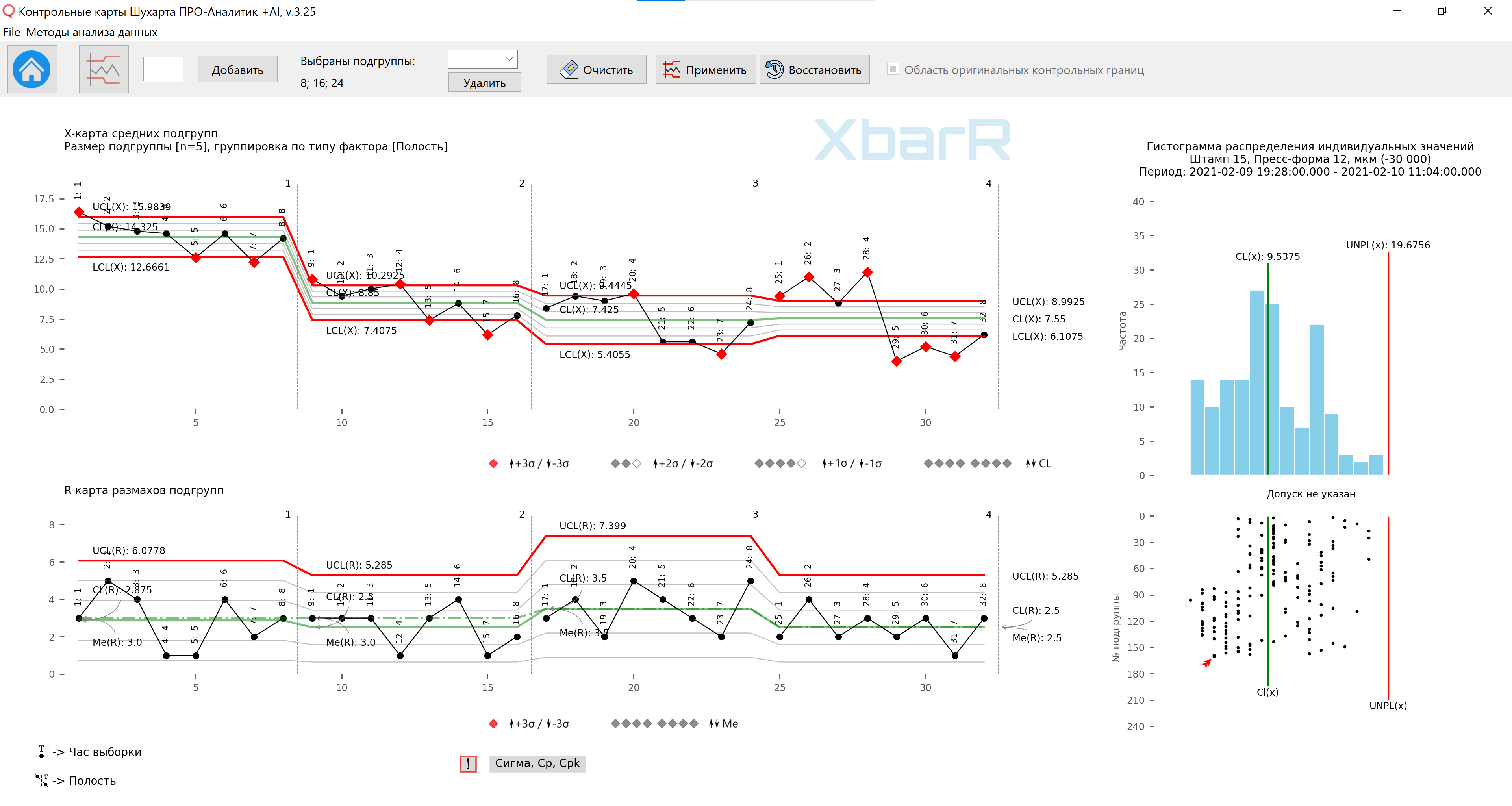
Рис. 13. Карта средних и размахов подгрупп для третьего способа организации данных в подгруппах с контрольными пределами для отдельных серий точек. Вертикальные линии разделения серий со значениями от 1 до 4 - № Полостей. Подписи всех точек - Час выборки. Рисунок подготовлен с использованием разработанного нами «Контрольные карты Шухарта ПРО-Аналитик +AI (для Windows, Mac, Linux)» с использованием уникальной функции автоматизации рациональной группировки данных для построения XbarR-карты средних и размахов подгрупп по выбранному типу источников вариаций (столбцу с факторами) и размеру подгрупп с применением функции построения контрольных границ для отдельных серий подгрупп .
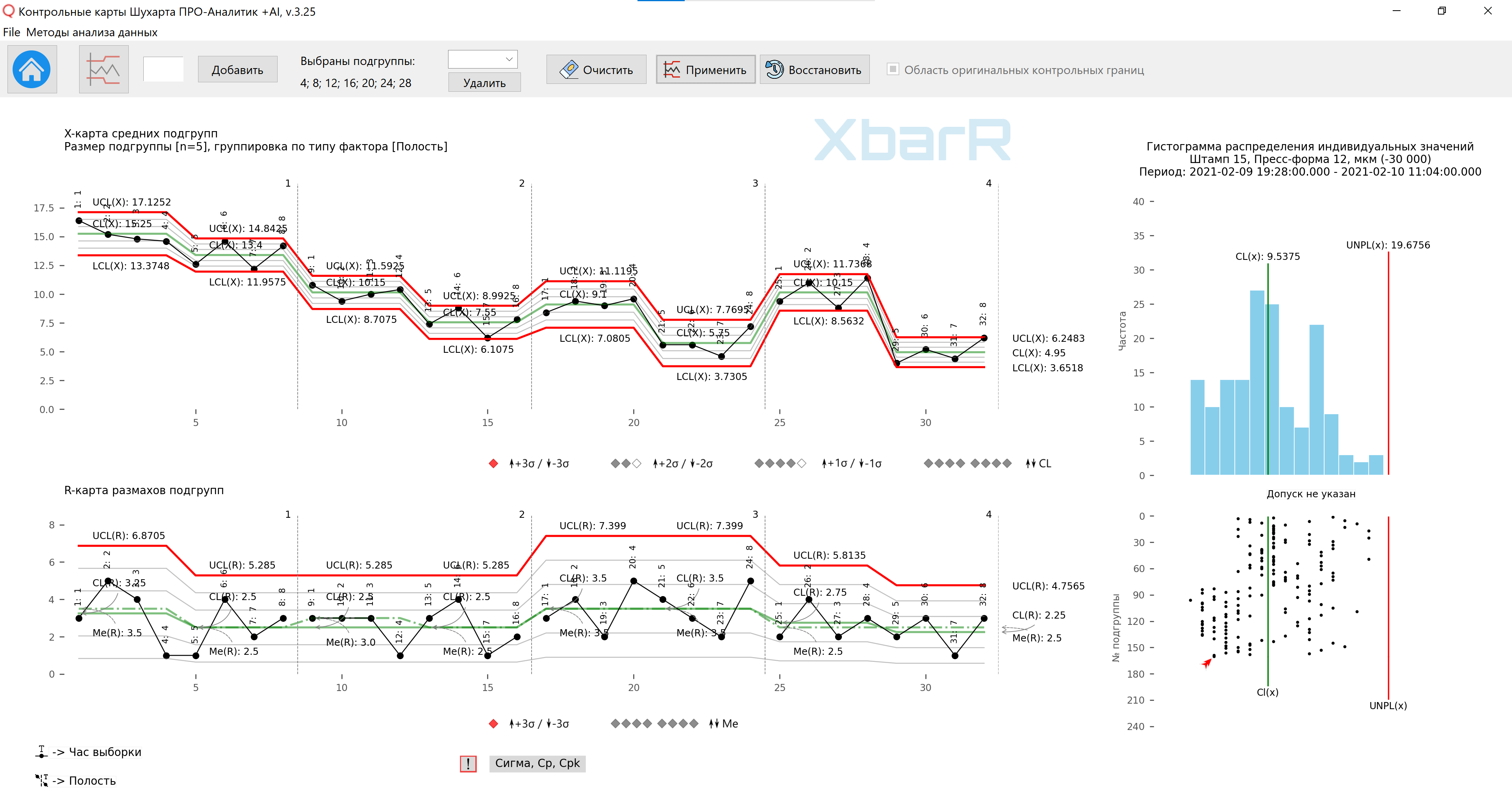
Рис. 14. Карта средних и размахов подгрупп для третьего способа организации данных в подгруппах с контрольными пределами для отдельных серий точек. Вертикальные линии разделения серий со значениями от 1 до 4 - № Полостей. Подписи всех точек - Час выборки. Рисунок подготовлен с использованием разработанного нами «Контрольные карты Шухарта ПРО-Аналитик +AI (для Windows, Mac, Linux)» с использованием уникальной функции автоматизации рациональной группировки данных для построения XbarR-карты средних и размахов подгрупп по выбранному типу источников вариаций (столбцу с факторами) и размеру подгрупп с применением функции построения контрольных границ для отдельных серий подгрупп .
Резюме. Организация данных в подгруппах
Хотя все три способа организации этих данных в подгруппы технически верны, они не эквивалентны практически. Разные организации задают разные вопросы о данных и делают разные предположения относительно данных.
Первый способ организации данных в подгруппы на рисунках 7 и 8 проверяет согласованность от полости к полости и ищет различия между часами и циклами.
Второй способ организации данных в подгруппы на рисунках 9 и 10 проверяет согласованность от цикла к циклу и ищет различия между часами и между полостями. Почему эта организация более чувствительна, чем первая?
Третий способ организации данных в подгруппы на рисунке 11 и 12 также проверяет соответствие от цикла к циклу и ищет различия между часами и между полостями, но, размещая полости на отдельных диаграммах (рисунок 12), легче выявлять почасовые и ежедневные различия в этом процессе. Из трех способов организаций этих данных лучше всего подходит третий.
Рациональное группирование данных
Ключом к тому, чтобы получить ответы на ваши вопросы на карте средних значений и размахов подгрупп, является понимание того, как две части XbarR-карты задают разные вопросы. Вы контролируете вопросы с помощью того, какие источники вариации вы размещаете внутри подгрупп и какие источники вариации вы размещаете между подгруппами. Вещи, которые могут отличаться друг от друга, должны находиться в разных подгруппах. Вещи, которые могут быть одинаковыми, должны находиться в одной и той же подгруппе.
Когда мы помещаем , например, два измерения вместе в одну и ту же подгруппу (n=2), мы делаем вывод, что эти два значения были получены при практически одинаковых условиях. Именно этот элемент суждения делает вашу подгруппу рациональной. Без такого суждения ваша подгруппа вполне может быть иррациональной.
Вы никогда не должны сознательно группировать непохожие вещи вместе. Каждая подгруппа должна быть логически однородной. Если вы соедините вместе яблоки, апельсины и бананы, вы можете получить хороший фруктовый салат, но у вас будут плохие подгруппы. К счастью, карта размахов может предупредить вас, когда вы систематически объединяете разные вещи в подгруппах. На рисунке 15 показана карта размахов с рисунка 8. Там у нас были все четыре полости в каждой подгруппе.

Рис. 15. Карта размахов подгрупп для первого способа организации данных в подгруппы.
Выделенная полоса на рисунке 15 представляет собой полосу одной сигмы. Мы ожидаем, что от 60 до 75 процентов значений диапазона попадут в этот диапазон. Здесь мы получаем 36 из 40, что составляет 90 процентов в пределах одной сигмы от центральной линии. Когда групповые размахи охватывают центральную линию, это свидетельствует о наличии подгрупп, сгруппированных вместе непохожих вещей. Обычная признак этого явления - 15 последовательных размахов в пределах одной сигмы от центральной линии карты размахов. Если вы обнаружите это, проверьте возможное расслоение внутри подгрупп. Чтобы понять, как стратификация внутри подгрупп влияет на карту средних, сравните контрольные пределы карты средних на рисунке 8 (в основном от LCL=4 до UCL=15) с таковыми на рисунке 10 (в основном от LCL=8 до UCL=11).
Сведите к минимуму разброс внутри подгрупп. Уровень фонового шума определяется вариациями внутри подгрупп. Любые сигналы придется искать на этом фоне шума. Минимизируя вариации внутри подгрупп, вы максимально увеличиваете чувствительность контрольной карты поведения процесса.
Максимально увеличьте возможность вариации между подгруппами. Это требует размышлений о том, какие типы потенциальных сигналов могут возникать в вашем потоке данных. Если вы хотите сравнить две вещи, их нужно поместить в разные подгруппы. Если есть вероятность, что две вещи могут быть разными, они должны принадлежать к разным подгруппам.
Не хороните сигналы внутри подгрупп. Группирование эффективно только в той степени, в которой подгруппы остаются однородными. Во многих областях статистики, где оценка параметров является целью, предпочтительны большие объемы данных. Но это не относится к XbarR-картам средних и размахов подгрупп. Увеличение размера подгруппы - хороший способ разрушить однородность подгрупп. Поскольку вычисления явно предполагают внутреннюю однородность подгрупп, логическая однородность подгрупп гораздо важнее, чем размер подгруппы.
Уважайте контекст ваших данных. Контекст определяет структуру ваших данных и является ключом к обнаружению особых причин вариаций при изменении вашего процесса. Даже порядок подгрупп может иметь значение. Вот почему мы обычно используем временной порядок для графика. Однако вы можете использовать другие порядки, если они имеют значение в контексте данных.
Контрольный вопрос
Какое неявное предположение на рисунках 8 и 10 оказалось ошибочным?
Наше программное обеспечение «Контрольные карты Шухарта ПРО-Аналитик +AI (для Windows, Mac, Linux)» уже содержит подготовленный файл Excel с данными для этой статьи.