Природа вариабельности (вариаций, изменчивости) - основа статистического мышления отличного от мышления в понятиях допусков
Этот раздел сайта посвящен объяснению необходимости понимания природа вариабельности для управления любыми системами (социальными, деловыми, производственными и техническими), ведь мы живем в мире, наполненном вариабельностью. Значимость понимания законов вариабельности для совершенствования качества и повышения эффективности производства и услуг трудно переоценить, эти знания так же важны, как и понимание законов аэродинамики, если вы занимаетесь проектированием самолётов.
Материал подготовил: научный директор Центра AQT Григорьев С. П..
Бесплатный доступ к статьям нисколько не уменьшает ценности изложенных в них материалов.
Вариабельность – изменчивость, разнообразие, разброс или мера отклонения от "оптимума". Само изменение называют вариацией или вариантом.
"Основная проблема менеджмента, лидерства и производства, как её сформулировал мой друг Ллойд Нельсон и как мы многократно подчёркивали, заключается в непонимании природы вариаций и неумении её интерпретировать.
Усилия и применение методов совершенствования качества и производительности в большинстве компаний и правительственных учреждений фрагментарны, не предполагают ни общего компетентного руководства, ни цельной системы непрерывного совершенствования.
Каждому, независимо от занимаемой должности, необходимо обучение и развитие. В атмосфере разрозненности усилий люди движутся каждый в своем направлении, не имея возможности приносить бóльшую пользу компании и тем более развиваться".
Важно понимать природу вариабельности, до того как приступать к любым изменениям в системе или бизнес-процессах компании по следующим причинам:
"Во-первых, если выход процесса определяется влиянием особых причин, то его поведение меняется непредсказуемо и, таким образом, невозможно оценить результат изменений в конструкции, обучении, политике закупок комплектующих и т. д., которые могли бы быть введены менеджментом в этот процесс (или в систему, которая содержит этот процесс) с целью улучшения. Пока процесс находится в неуправляемом состоянии, никто не может предсказать его возможности".
"Во-вторых, когда особые причины устранены, так что остаются только общие причины вариаций, тогда улучшения могут зависеть от управляющих воздействий. Поскольку в этом случае наблюдаемые вариации системы определяются тем, как и каким образом, процессы и система были спроектированы и построены, то только управляющий персонал, топ-менеджеры имеют полномочия для изменений системы и процессов".
"Ну, и какая разница? И что нам это дает? Да все то, что отделяет успех от неудачи! В-третьих, мы приходим к проблеме, если мы (на практике) не отличаем один тип изменчивости от другого и действуем без понимания, мы не только не улучшим дело — мы, несомненно, сделаем положение еще худшим. Ясно, что это так и будет, и останется загадкой для тех, кто не понимает природы изменчивости (вариаций)".
Статистически управляемое (стабильное) состояние процесса
Рисунок 1. [4] Демонстрация распределения данных и соответствующая контрольная XbarR-карта (XR-карта) Шухарта средних и размахов подгрупп для предсказуемого (статистически управляемо процесса). Красные линии, соответственно, верхняя (Upper Control Limit, UCL, ВКГ) и нижняя (Lower Control Limit, LCL, НКГ) контрольные границы. Зеленая линия - Центральная линии (Central Line, CL, ЦЛ) - среднее значение.
Когда построенные для анализируемого выхода процесса контрольные карты демонстрируют статистически устойчивое состояние, в этом случае крайне нежелательно вмешательство в процесс с целью разобраться с каждым скачком вверх и вниз, привлекающим внимание.
Видео 1. Эксперимент с доской Гальтона демонстрирует явление вариабельности статистически управляемого процесса в замкнутой системе при идеальных условиях.
По сути, все точки между контрольными границами стабильного процесса являются однородными. Попытки разобраться с худшими значениями в этом случае будут выдавать лишь ложные предположения и вы в очередной раз впустую потратите драгоценное рабочее время.
Видео 2. Эксперимент с доской Гальтона пояснение роли вариабельности на примере статистически управляемого (стабильного) процесса, функционирующего шире поля допуска. LSL (Lower Specification Limit) - нижняя граница поля допуска, USL (Upper Specification Limit) - верхняя граница поля допуска.
Подобно шарикам в эксперименте с доской Гальтона плотность распределения контролируемых значений в стабильной системе распределяется случайным образом вокруг центральной линии (линии среднего) процесса. Все "шарики" попадают в те или иные "карманы" совершенно случайно. Хотите вы того или нет, будут шарики в карманах слева, в центральной части и справа, а количество шариков в карманах будет соответствовать эмпирическому правилу распределения значений в стабильной системе.
"Любые два числа, которые не являются одинаковыми, считаются разными. К сожалению, это верно, когда речь идёт об арифметике, но неверно, когда речь заходит об интерпретации данных. В этом мире два разных числа вполне могут представлять одно и то же".
Например, когда процесс находится в статистически управляемом состоянии не имеет практического смысла разбор каждого случая выхода продукции за пределы допуска (спецификации), т. к. в этом случае дефектная и качественная продукция являются однородными продуктами стабильного процесса. С таким же успехом (безуспешно) вы можете анализировать и продукцию, находящуюся в пределах допуска. Эта ошибочная практика наблюдается повсеместно:
"По всем случаям брака назначается расследование. Инженер по качеству выясняет корневую причину возникновения дефекта. В большинстве своем высокий уровень качества достигается путем постоянных изменений в техпроцессе".
Очередной раз подтверждается то, что говорил Деминг:
"Знаниям нет замены. Но перспектива использования знаний пугает".
Статистически управляемое состояние процесса, лучшее на что он способен в текущих условиях. В этом случае знание о прошлом поведении процесса дает основания для прогнозирования его будущего поведения, пока он находится в статистически устойчивом состоянии.
Для совершенствования (уменьшения вариабельности и смещения положения среднего ближе к номиналу) стабильных процессов необходимы системные изменения. Такие изменения, если они имеют значимый эффект, будет легко отследить с помощью контрольных карт.
Установка конкретной численной цели выше или ниже контрольных границ (ВКГ, НКГ) для предсказуемых (управляемых) процессов тем более бессмысленна. Процесс, по определению предсказуем. Под действием общих (системных, случайных) причин процесс будет случайным образом выдавать однородные точки выше и ниже центральной линии (ЦЛ) в соответствии с эмпирическим правилом плотности распределения (будет пояснено ниже). Новые точки стабильного процесса будут вписываться в рассчитанные контрольные пределы (ВКГ, НКГ) все меньше оказывая влияние на арифметическое значение центральной линии.
Рисунок 2. Численная цель для стабильного процесса не имеет смысла. Контрольная карта Шухарта для статистически управляемого (стабильного) процесса. Красные линии, соответственно, верхняя (Upper Control Limit, UCL, ВКГ) и нижняя (Lower Control Limit, LCL, НКГ) контрольные границы. Зеленая линия - Центральная линии (Central Line, CL, ЦЛ) - среднее значение.
Непревзойденным инструментом управления совершенствованием процесса являются Контрольные карты Шухарта. Контрольные границы карт Шухарта служат в роли операционального определения минимизации потерь от совершения ошибок первого и второго рода, являются голосом ваших процессов, а также позволяют объективно отслеживать реальные изменения процессов как в лучшую, так и в худшую сторону.
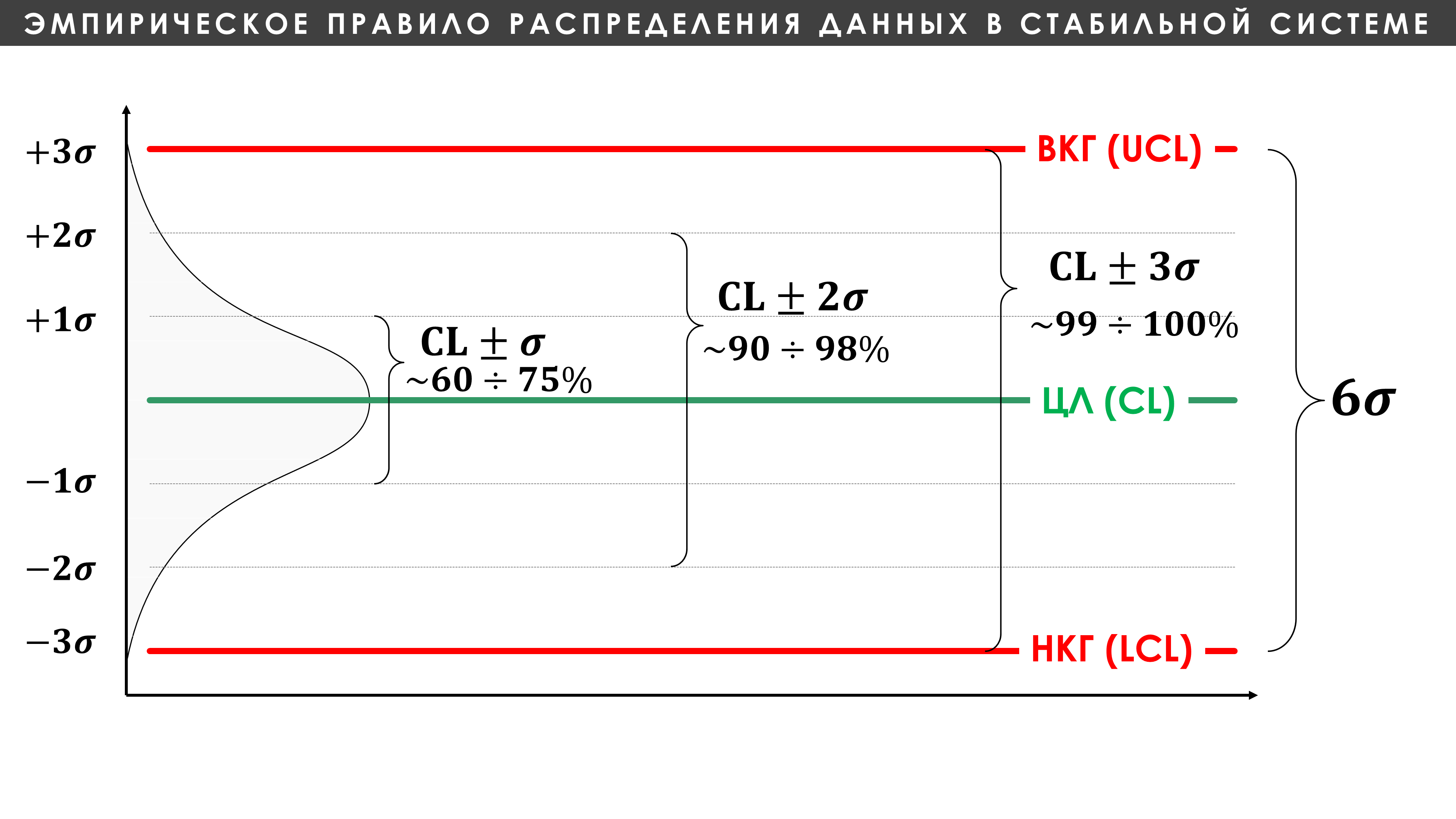
Рисунок 3. Эмпирическое правило распределения данных в стабильной системе. Контрольная карта Шухарта. Красные линии, соответственно, верхняя (Upper Control Limit, UCL, ВКГ) и нижняя (Lower Control Limit, LCL, НКГ) контрольные границы. Зеленая линия - Центральная линии (Central Line, CL, ЦЛ) - среднее значение.
"Эмпирическое правило предоставляет нам полезный способ описания данных при помощи меры положения и меры
рассеяния. Если дано однородное множество данных, тогда:
1) примерно 60–75% данных находятся в пределах одной сигма-единицы по обе стороны от среднего;
2) ориентировочно от 90 до 98% данных лежат на расстоянии две сигма-единицы от среднего;
3) приблизительно 99–100% данных удалены от среднего не более чем на три сигма-единицы.
Сигма-единица (σ) — это мера масштаба данных. Общие статистики рассеяния можно преобразовать в (σ)-единицы при помощи опубликованных формул*".
* Формулы для расчёта σ-единиц см. [11.1] ГОСТ Р 50779.42-99 (ИСО 8258-91) - Примечание Григорьев С. П.
Видео 3. Эмпирическое правило распределения значений в стабильной системе. Контрольная карта Шухарта для эксперимента с доской Гальтона. Красные линии, соответственно, верхняя (Upper Control Limit, UCL, ВКГ) и нижняя (Lower Control Limit, LCL, НКГ) контрольные границы. Зеленая линия - Центральная линии (Central Line, CL, ЦЛ) - среднее значение.
Видео 3 с эмпирическим правилом распределения значений в стабильной системе доказывает отсутствие научного и практического смысла в утверждении о том, что границы [+/- 2σ] являются предупредительными границами. Малая часть однородных значений должна оказаться за этими границами стабильного процесса в любом случае. А действительными сигналами служат точки на контрольной карте Шухарта определяемые в соответствии с зональными критериями Western Electric.
Более того, [4] Дональд Уилер в книге "Статистическое управление процессами. Оптимизация бизнеса с использованием контрольных карт Шухарта" демонстрирует шесть теоретических распределений данных, и для всех распределений границы [+/- 2σ] не являются предупредительными. Для равномерного распределения - они могли бы быть границами действий, а для оставшихся за исключением нормального распределения, только граница [- 2σ] могла бы быть нижней границей действий (нижней контрольной границей, LCL), но в реальном мире мы никогда не знаем истинной модели (формы) распределения анализируемого параметра. Смотрите анимацию 1.
Анимация 1. Шесть теоретических распределений данных с указанием стрелками границ [+/- 2σ].
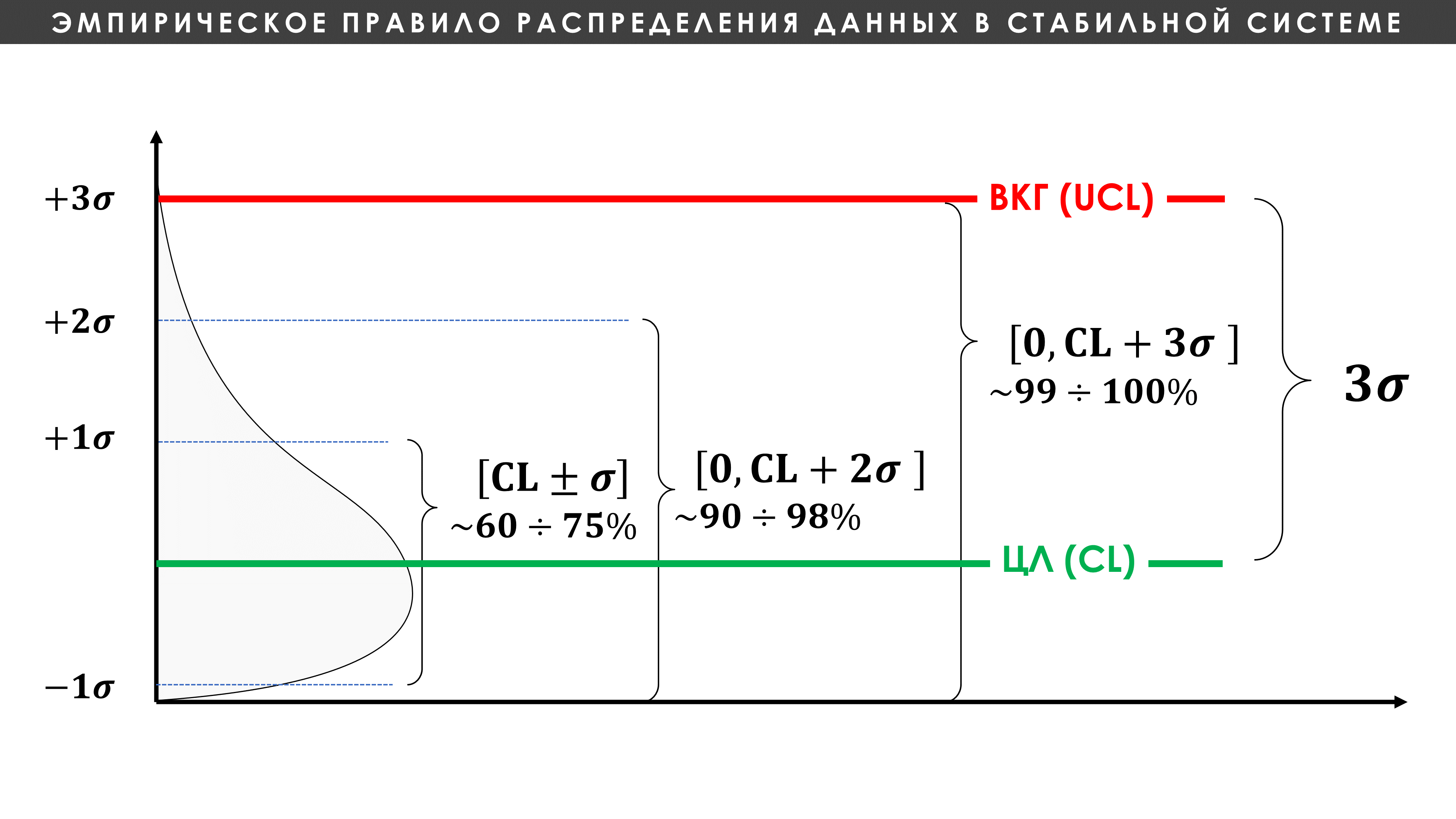
Рисунок 4. Пример частного случая применения эмпирического правила распределения данных в стабильной системе для процесса с одной контрольной границей. Контрольная карта Шухарта. Красная линия - верхняя (Upper Control Limit, UCL, ВКГ). Зеленая линия - Центральная линии (Central Line, CL, ЦЛ) - среднее значение.
"Канбан, или система «точно вовремя», – это естественное следствие достижения состояния статистического управления для показателей качества продукции, что, в свою очередь, ведет к достижению статистической управляемости для скорости производственного процесса".
Контрольные границы процесса "ничего не знают" о границах допуска (требованиях спецификаций), относительно которых определяется дефектность изделий. Дефектность продукции определяется искусственно установленными границами допусков или спецификаций. Раздвиньте границы спецификации шире контрольных границ статистически управляемого процесса - вот вам и "ноль дефектов" или "бездефектное производство". Был "ноль дефектов", сблизьте границы спецификации разместив их внутри контрольных границ карты Шухарта - вот вам и гарантированные "дефекты", вероятное количество которых легко предсказать по эмпирическому правилу распределения данных в стабильной системе.
Какие действия не следует, а какие действительно стоит предпринять по отношению к процессу производящему дефектную продукцию представлен материал в статье: Правильные и неправильные пути использования полей допусков. Следует ли сортировать продукцию относительно полей допуска на дефектную и бездефектную или пытаться настраивать процесс?.
"Соответствия допускам недостаточно.
Более того, не существует способа узнать, сохранится ли соответствие допускам, если процесс не находится в состоянии статистической управляемости. До тех пор пока особые причины не определены и не исключены (по крайней мере, те, что появлялись до сих пор), никто не сможет предсказать, что произведет процесс в следующий час.
Зависимость от инспекции (единственная альтернатива) опасна и дорогостояща. Ваш процесс может хорошо работать с утра и произвести изделия за границами поля допуска после полудня.
Рассчитанные допуски – это не границы, определяющие, как действовать. На деле крупные потери возникают тогда, когда процесс постоянно регулируется то одним, то другим образом с целью соответствия допускам".
Статистически неуправляемое (непредсказуемое) состояние процесса
Рисунок 5. [4] Демонстрация распределения данных и соответствующая контрольная XbarR-карта (XR-карта) средних и размахов подгрупп для процесса, не меняющегося во времени, находящегося в статистически управляемом состоянии (стабильного процесса). Красные линии, соответственно, верхняя (Upper Control Limit, UCL, ВКГ) и нижняя (Lower Control Limit, LCL, НКГ) контрольные границы. Зеленая линия - Центральная линии (Central Line, CL, ЦЛ) - среднее значение.
Четыре точки в зоне каждой гистограммы (колоколообразные кривые) на рисунке 1.2. - индивидуальные значения и представляют одну подгруппу данных. Точки на контрольной Xbar-карте средних (верхний график) представляют средние значения точек каждой подгруппы из соответствующих гистограммам. Точки на R-карте размахов подгрупп (нижний график) представляют размах подгруппы (разницу между максимальным и минимальным значением в каждой подгруппе). Все точки на графиках контрольной XbarR-карты размещены слева направо по мере образования значений во времени.
Видео 4. Эксперимент с доской Гальтона пояснение роли вариабельности на примере статистически неуправляемого процесса, периодически меняющего свое положение относительно поля допуска. LSL (Lower Specification Limit) - нижняя граница поля допуска, USL (Upper Specification Limit) - верхняя граница поля допуска.
Статистически неустойчивое (непредсказуемое, неуправляемое, нестабильное) состояние процесса может быть выявлено с помощью контрольных карт Шухарта. Это худшее состояние для любых процессов.
Когда контрольные карты демонстрируют признаки нестабильного состояния процесса, только в этом случае требуется немедленное вмешательство в процесс для выявления и устранения особых причин, вызвавших эту нестабильность.
"Если система не находится в состоянии статистической управляемости, трудно измерить эффект от изменений. Говоря точнее, если нет управляемости, заметны будут только катастрофические результаты".
Системные изменения, вносимые в неуправляемый процесс, скорее всего, окажутся малополезными для совершенствования процесса и будут экономически нецелесообразны. Более того, если процесс, в который планируется внести изменения с целью его улучшения, находится в статистически неуправляемом состоянии не будет возможности достоверно измерить эффект от таких изменений.
Прежде всего потребуется привести процесс в статистически устойчивое состояние, что уже само по себе всегда приводит к существенному экономическому эффекту и не требует дополнительных трат.
Установка конкретной численной цели для непредсказуемого процесса больше напоминает профанацию.
Рисунок 6. Численная цель для непредсказуемого процесса подобна гаданию на кофейной гуще.
Контрольная карта Шухарта для статистически неуправляемого (нестабильного) процесса.
Красные линии, соответственно, верхняя (Upper Control Limit, UCL, ВКГ) и нижняя (Lower Control Limit, LCL,
НКГ) контрольные границы. Зеленая линия - Центральная линии (Central Line, CL, ЦЛ) - среднее значение, 𝝈 -
мера разброса данных (расчетная величина присущая конкретному уникальному процессу).
Литература:
- [11] ГОСТ Р ИСО 7870-1-2011 (ISO 7870-1:2007), ГОСТ Р ИСО 7870-2-2015 (ISO 7870-2:2013) - Статистические методы. Контрольные карты Шухарта. Скачать (PDF) 7870-1, 7870-2.
- [11.1] ГОСТ Р 50779.42-99 (ИСО 8258-91) Статистические методы. Контрольные карты Шухарта (версия до выхода ГОСТ 7870-1, 7870-2) - мы в DEMING.PRO предпочитаем эту версию. Скачать (PDF) 50779.42-99.
- [12] ГОСТ 51814.3-2001 – Системы качества в автомобилестроении. Методы статистического управления процессами. Скачать (PDF) 51814.3.
Статья: Правила определения отсутствия управляемости по контрольным картам.
В коротком видео ниже представлена дорожная карта экономически целесообразного метода совершенствования процесса до состояния, когда процесс будет функционировать так узко в границах установленных допусков, что не будет производить дефектных изделий вообще. Эта цель процесса легко нейтрализует неопределенность измеряемых значений из-за ошибки системы измерений, которая в свою очередь должна находиться в стабильном состоянии, т. к. не будет граничных значений размещенных у границ допусков.
О граничных значениях представлен материал в статье: Соответствующая спецификации (допуску) продукция действительно соответствующая? А дефектная продукция действительно дефектная?.
Видео 5. Что же надо делать для совершенствования процессов?
Условные обозначения элементов в видео: НГД и ВГД - нижняя и верхняя границы допуска соответственно (анг,
LSL и USL); m0 - номинал поля допуска; НГП и ВГП - нижняя и верхняя натуральные границы процесса (англ. LNPL
и UNPL); ЦЛ - центральная линия процесса (среднее процесса).
Смотрите описание Функции потерь качества Тагути, дающее операциональное определение качества мирового класса.
Диагностирование действительных изменений в процессе
Ниже представлен фильм о методе оперативного диагностирования изменений в процессе (системе), как положительных, так и отрицательных, с помощью контрольной карты Шухарта.
Видео 6. Метод оперативного диагностирования изменений в процессе с помощью Контрольных карт Шухарта. Красные линии, соответственно, верхняя (Upper Control Limit, UCL, ВКГ) и нижняя (Lower Control Limit, LCL, НКГ) контрольные границы. Зеленая линия - Центральная линии (Central Line, CL, ЦЛ) - среднее значение.
Смотрите описание экспериментов «воронка и мишень» и «красные бусины» — превосходные демонстрации природы вариаций и обычной практики менеджмента.